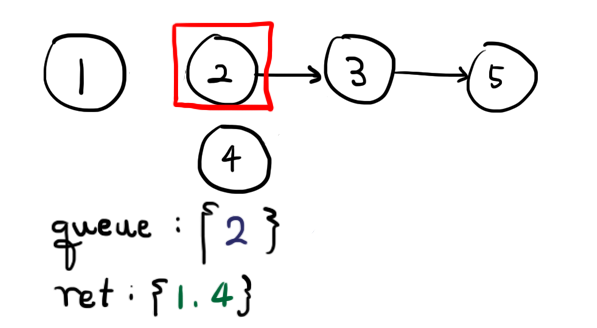
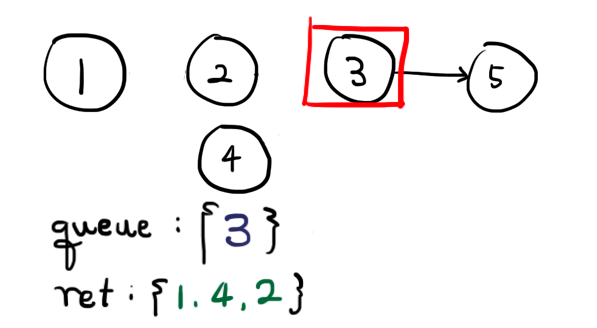
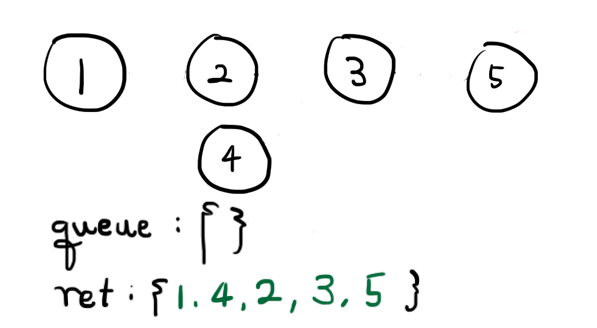eff3ct's st0rage Dev Blog

제 6회 HCPC Beginner Division PS일지

08 Nov 2021

제 6회 HCPC Beginner Division

11월 말에 HCPC가 있다고해서 연습좀 해볼겸 이미 나온 기출 셋을 한 번 돌아보기로 했다. 지금까지(11-08, 17시) 1문제 TLE고 나머진 AC를 받았다. 예전부터 DP가 넘 어려웠는데 아직도 그런거 같다. 왜냐면 TLE때문에 못푼 단 하나의 문제가 DP임..ㅋㅋ 여튼 DP 공부좀 열심히 해야겠다는 생각이 드는 그런 셋이었다.

A번 : 과제는 끝나지 않아! / BOJ 17952

Tier : Silver III
설명 보기

간단한 구현 문제이다. 문제에서 시키는대로 구현하면 AC를 받을 수 있다. 이때, 이전회차에 그만둔 과제를 이어서 해야하니 선입후출 특징을 가지는 자료구조가 있으면 편리하다. 그게 딱 스택에 해당하니, 스택을 사용해서 문제에 나와있는것을 그대로 구현해주면 된다.

코드 보기 
int main() {
    int ret = 0;
    int N; cin >> N;
    stack<pair<int, int>> stk;
    int score = 0, time = 0;
    for(int i = 0; i < N; ++i) {
        int cmd; cin >> cmd;
        
        if(cmd == 1) {
            if(time > 0) stk.push({score, time});
            cin >> score >> time;

            if(--time == 0) {
                ret += score;

                if(!stk.empty()) {
                    score = stk.top().first;
                    time = stk.top().second;
                    stk.pop();
                }
            }
        }
        else {
            if(--time == 0) {
                ret += score;
                if(!stk.empty()) {
                    score = stk.top().first;
                    time = stk.top().second;
                    stk.pop();
                }
            }
        }
    }

    cout << ret;

    return 0;
}

B번 : 흩날리는 시험지 속에서 내 평점이 느껴진거야 / BOJ 17951

Tier : Gold IV
설명 보기

그룹으로 나눠서 각 그룹별 합의 최소값이 최대가 되어야하도록 만드는 문제이다. 난 처음에 생각없이 전체 합 / 그룹 수 = 평균이라는 식을 써서 이 평균값보다 커지는 최초의 원소에서 끊기도록 그룹을 나눴는데.. 뭐 증명도 없이 풀었기에 당연하게도 WA. 끝 그룹에서 극단적인 case가 나올수도 있고 여러모로 반례가 많은 풀이이니 당연히 안된다. 여튼, 그래서 좀 생각을 해보니 이분탐색으로 값을 찾아주면 되는거 아닌가 싶어 그렇게 코드를 짰다. 각 그룹의 합이 최소 mid보다 크도록 해서 그룹을 나누고, 그 다음 나눠진 그룹의 수로 range를 줄여나가는 식으로 하면, count >= 그룹의 수 일때, 답의 후보가 발생한다. 그 때마다 값을 갱신하면, 마지막에 저장된 값이 곧 답이된다. 즉, 파라메트릭 서치로 요로로콤 해결할 수 있는 문제였다.

코드 보기 
#include <iostream>
#include <cmath>
#include <vector>

using namespace std;

int solve(vector<int>& seq, int K) {
    int r = 20 * 1e5;
    int l = 1;

    int ret = -1;

    while(l <= r) {
        int partition = 0;
        int mid = (l + r) / 2;
        int cnt = 0;

        for(int i = 0; i < (int)seq.size(); ++i) {
            partition += seq[i];
            if(partition >= mid) {
                cnt++;
                partition = 0;
            }
        }

        if(cnt >= K) {
            ret = mid;
            l = mid + 1;
        }
        else r = mid - 1;
    }

    return ret;
}

int main() {
    int N, K; cin >> N >> K;
    vector<int> seq(N);

    for(int i = 0; i < N; ++i) cin >> seq[i];

    cout << solve(seq, K);

    return 0;
}

C번 : Drop The Byte! / BOJ 17949

Tier : Bronze I
설명 보기

문제에서 시키는대로 하면 된다. char이면 2자리, int면 8자리, long_long이면 16자리씩 string을 끊어주고, 그 끊어준 string을 10진수로 convert하면 AC. 뭔가 16진수 string -> 10진수 string으로 바꿔주는게 있을 법 한데, 나는 그냥 map을 써서 직접 변환시켜주는 식으로 풀었다. 그러나, 난 처음에 이거 TLE받았는데, 처음엔 그냥 진짜 substr로 string을 잘랐기 때문에 그랬다. 빠르게 하기 위해서 인덱스를 저장해두고 자른 효과를 주는 식으로 바꾸었더니 AC.

코드 보기 
#include <iostream>
#include <map>
#include <string>

using namespace std;

map<char, long long> convert = { {'0', 0}, {'1', 1}, {'2', 2}, {'3', 3}, {'4', 4}, {'5', 5}, {'6', 6}, {'7', 7}, {'8', 8}, {'9', 9}, {'a', 10}, {'b', 11}, {'c', 12}, {'d', 13}, {'e', 14}, {'f', 15} };

long long calc(string& s, int idx, int sz) {
    long long ret = 0;
    long long size = 1;

    for(int i = idx + sz - 1; i >= idx; --i) {
        ret += convert[s[i]] * size;
        size *= 16;
    }

    return ret;
}

int main() {
    ios_base::sync_with_stdio(false);
    cin.tie(nullptr);
    cout.tie(nullptr);

    string str; cin >> str;
    int N; cin >> N;
    int idx = 0;
    for(int i = 0; i < N; ++i) {
        string cmd; cin >> cmd;

        if(cmd == "char") {
            cout << calc(str, idx, 2) << " ";
            idx += 2;
        }
        else if(cmd == "int") {
            cout << calc(str, idx, 8) << " ";
            idx += 8;
        }
        else {
            cout << calc(str, idx, 16) << " ";
            idx += 16;
        }
    }

    return 0;
}

D번 : 퐁당퐁당 1 / BOJ 17944

Tier : Bronze III
설명 보기

간단한 문제다. 뭐 잡다한 설명이 많은데, 그냥 1 2 3 … 2n - 1 2n 2n -1 … 3 2 1 2 3 … 이런 수열의 특정 항을 구하는 문제로 정리해볼 수 있겠다. 수열 생긴 꼴을 보면 음 뭔가 모듈러로 \(\scriptsize O(1)\)만에 특정번째 항을 구해낼 수 있을 것 같다. 일반항을 찾다보니까 좀 껄끄로워서.. ㅋㅋ 아예 찾아가는식으로 구현했다 그냥. 그래서 아래 코드는 복잡도가 \(\scriptsize O(T)\)이다.

코드 보기 
#include <iostream>

using namespace std;

int main() {
    int N, T; cin >> N >> T;
    int ret = 0;
    bool flag = false;
    for(int i = 0; i < T; ++i) {
        if(ret == 2 * N) flag = true;
        else if(ret == 1) flag = false;

        if(flag) ret--;
        else ret++;
    }

    cout << ret;
    return 0;
}

E번 : 뜨끈한 돼지국밥 / BOJ 17948

Tier : Platinum III
설명 보기

아직 TLE라 해결하지 못했지만, 중간 풀이를 남겨보려 한다.

2021-11-08-17시 기준으로 \(\scriptsize O(n ^ {4})\) 정도의 DP 풀이를 만들어낼 수 있었다. 이 문제를 해결하기 위해서는 \(\scriptsize O(n ^ {2})\) 까지는 줄여야해서.. 아직 터무니없이 복잡도가 높다. 먼저 \(\scriptsize cost(count, x) = "count번째 국밥집을 x주소에 놓았을 때 최소 비용"\) 이라고 정의했다. 그럼, \(\scriptsize cost(count, x) = min(cost(count, x), cost(count - 1, k) + newSummation + m) (k < x)\)이라고 할 수 있다. 이때, newSummation은 x주소에 국밥집을 놓으면서 변화하는 거리비용을 의미한다. 즉, 주소 k 국밥집보다 주소 x 국밥집에 더 가까우면 원래 있던 값을 빼줘야하니 빼고, 수정된값으로 바꿔놓아야하니 그 값들을 모두 합친게 newSummation이다. count가 하나 증가할때마다 m이 하나씩 증가하니 m도 하나 증가시켜주면 된다.

이런식으로 구하면 cost(count, x) 테이블을 채우는데에 \(\scriptsize O(n ^ {3})\)이고, newSummation을 구하는데에 \(\scriptsize O(n)\)이라 \(\scriptsize O(n ^ {4})\)라 TLE이다. 그래서 아직까지 실패했으나, 그래도 풀이를 남기는게 의미있을듯 싶어 남겨본다.

코드 보기 
#include <iostream>
#include <vector>
#include <cmath>
#include <algorithm>

#define INF 12345678987654321LL

using namespace std;
typedef long long ll;

void solve(vector<ll>& address, ll N, ll C, ll M) {
    //dp[count][x] = x위치에 count번째 사업장을 놓을때 최소 cost

    //ret = min(dp[count][x], ret), ret init = inf

    //dp[count][x] = min(dp[count - 1][k < x] + C * summation(|x - update_loc|) 
    //                  - C * summation(|k - update_loc|) + m, dp[count][x])

    //dp init = inf

    //dp[1][x'] : for every x', dp[1][x'] = C * summation(|x' - loc|) + m
    //5000 * 5000 vector -> x는 N에서 유효한 좌표만 있으면 되기 때문에 최대 ~ 100MB
    ll ret = 12345678987654321LL;
    int retCnt = 1;

    sort(address.begin(), address.end());
    vector<ll> cpy(address);
    cpy.erase(unique(cpy.begin(), cpy.end()), cpy.end());

    vector<vector<ll>> dp(N + 1, vector<ll>(N + 1, INF));

    for(int i = 0; i < (int)cpy.size(); ++i) {
        ll s = 0;
        for(auto& element : address) s += abs(cpy[i] - element);
        dp[1][cpy[i]] = C * s + M;
        ret = min(ret, dp[1][cpy[i]]);
    }

    for(int count = 2; count <= N; ++count) {
        for(int loc = 0; loc < cpy.size(); ++loc) {
            for(int k = 0; k < loc; ++k) {
                ll sCur = 0, sLast = 0;
                for(auto& element : address) {
                    if(abs(element - cpy[k]) > abs(element - cpy[loc])) {
                        sCur += abs(cpy[loc] - element);
                        sLast += abs(cpy[k] - element);
                    }
                }

                dp[count][cpy[loc]] = min(dp[count][cpy[loc]], 
                dp[count - 1][cpy[k]] + C * sCur - C * sLast + M);
                
                if(dp[count][cpy[loc]] < ret) {
                    ret = dp[count][cpy[loc]];
                    retCnt = count;
                }
            }
        }
    }

    cout << ret << " " << retCnt;
}

int main() {
    ios_base::sync_with_stdio(false);
    cin.tie(nullptr);
    cout.tie(nullptr);
    
    ll N; cin >> N;
    vector<ll> address(N);
    for(int i = 0; i < N; ++i) cin >> address[i];
    ll C, M; cin >> C >> M;

    solve(address, N, C, M);

    return 0;
}

F번 : 피자는 나눌 수록 커지잖아요 / BOJ 17946

Tier : Bronze II
설명 보기

좀 황당한 문제랄까? 모든 테케에 대해 1만 출력하면 그게 답이다. 왜냐면, 자를때마다 최대 3개의 조각이 더 생기는데 이게 4개 이상부터는 줘야하는 갯수보다 작아지니까 특정횟수 이상부터는 음수값이 나온다. 여기선 최대로 먹을 수 있는 피자조각수라 했는데, 이걸 계산해보면 1보다 커질 수 없음을 쉽게 알 수 있다.

코드 보기 
#include <iostream>

using namespace std;

int main() {
    int N; cin >> N;

    while(N --> 0) {
        int K; cin >> K;
        cout << 1 << '\n';
    }

    return 0;
}

G번 : 투튜브 / BOJ 17954

Tier : Gold I
설명 보기

constructive proof 문제다. greedy하게 접근해보자면, 매 순간순간마다 빼낼 수 있는 원소중에서 가장 큰 원소를 꺼내도록 하면 부패도의 누적이 최소가 된다. 2N, 2N-1, 2N-2, 이 3개의 숫자는 가장 처음 빼내질 수 없는 수라는게 자명하다. 따라서, 2N-3부터 꺼내질 수 있다. 그렇게 하기 위해선 2N ~ 2N-2의 수가 모서리에 각각 하나씩 있어야 함을 알 수 있다. 그 다음으론 2N-4부터 쭉 빼낼 수 있도록 배치해주면 남은 수부터 큰 순으로 일렬로 배열되어야 한다는 사실을 깨달을 수 있다. 그럼 한 행에 단 하나의 원소가 남는 때가 오는데 그 때, 남은 원소가 2N, 2N-1, 2N-2중 하나가 된다. 큰수를 먼저 빼는게 유리하기에.. 그 행에 남은 한 원소는 2N-2이 되어야 부패도가 최소가 될 수 있음을 어렵지 않게 관찰할 수 있다. 그런 다음엔 순서대로 2N-1이 빠지고, 2N을 제외하고 나머지 원소들이 다 빠진후 2N이 빠지게 되어 부패도가 최소가 된다. 즉, 다음 그림처럼 원소를 배치하면 된다는 얘기이다.

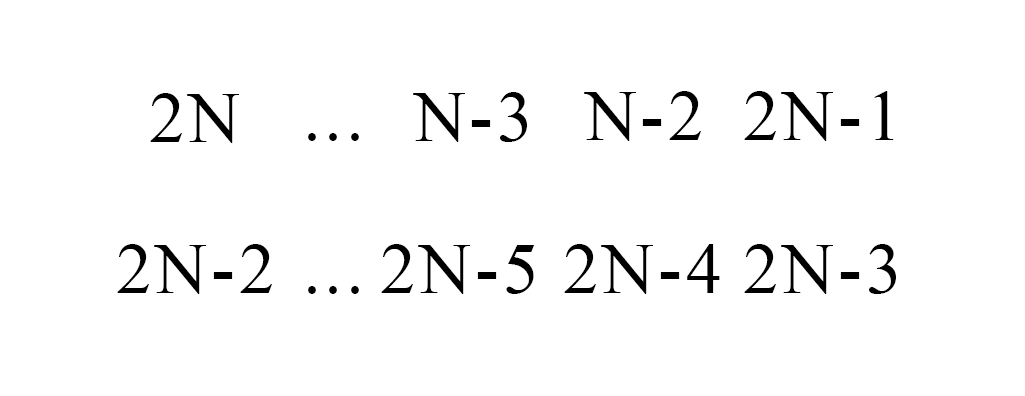
table

코드가 다소 지저분하긴 하나, 대충 요런식으로 배치를 구성한 뒤 직접 부패도를 계산해서 부패도와 함께 배치를 출력해주면 AC.

코드 보기 
#include <iostream>
#include <vector>

using namespace std;
typedef long long ll;

int main() {
    ios_base::sync_with_stdio(false);
    cin.tie(nullptr);
    cout.tie(nullptr);

    int N; cin >> N;

    vector<vector<int>> apple(2, vector<int>(N));

    if(N != 1) {
        apple[0][0] = 2 * N;
        apple[0][N - 1] = 2 * N - 1;
        apple[1][0] = 2 * N - 2;
        apple[1][N - 1] = 2 * N - 3;

        int col = N - 2;
        for(int i = 2 * N - 4; i > N - 2; --i) apple[1][col--] = i;

        col = N - 2;
        for(int i = N - 2; i > 0; --i) apple[0][col--] = i;

        ll time = 1;
        ll s = N * (2 * N + 1);
        ll ret = 0;

        ll now = 2 * N - 3;
        for(int i = 0; i < N - 1; ++i) {
            s -= now--;
            ret += s * time++;
        }

        now = 2 * N - 2;
        s -= now;
        ret += s * time++;

        now = 2 * N - 1;
        s -= now;
        ret += s * time++;

        now = N - 2;
        for(int i = 0; i < N - 2; ++i) {
            s -= now--;
            ret += s * time++;
        }

        cout << ret << '\n';

        for(int i = 0; i < 2; ++i) {
            for(int j = 0; j < N; ++j) {
                cout << apple[i][j] << ' ';
            }
            cout << '\n';
        }
    }
    else {
        cout << 2 << '\n';
        cout << 1 << '\n' << 2;
    }
 
    return 0;
}

H번 : 상남자 곽철용 / BOJ 17947

Tier : Gold I
설명 보기

문제 핵심 아이디어는 모듈러를 취했기에 그룹으로 각각의 수를 나눌 수 있다는 점이다. mod K에 대해 수를 모아보면, 각각 0 ~ K-1사이의 값을 가지게 된다. 곽철용이 뽑은 수가 A, B이고 점수를 \(\scriptsize score = \|A mod K - B mod K\|\) 라 할 수 있으니, 다른 사람들이 가능한 점수들 중에 score + 1 부터는 순서쌍이 몇개나 존재할 수 있는지만 알면 된다. score + 1부터 시작해서 K - 1까지 쭉 훑으면서 해당 카드들에 대응하는 카드가 몇개 있는지 세주고, 그 쌍이 M - 1개를 초과하면 M - 1명 모두 곽철용을 이길 수 있다는 의미이니, 그때는 값을 M - 1로 바꾸어 주면 해결. 해보면 알겠지만 이 쌍을 세는 과정이 그리 쉽지가 않아서.. 나도 다 풀어놓고 구현을 한참동안이나 계속 고쳐서 겨우 AC를 받아냈다. 다른 사람들 풀이를 보니 two-pointer를 사용해 하나씩 지우는 풀이가 많이 보이는듯 했다. 뭐 난 그렇게 풀진 않았지만, 여튼 그런방법으로도 순서쌍을 셀 수 있다.

코드 보기 
#include <iostream>
#include <vector>
#include <cmath>

using namespace std;

int main() {
    int N, M, K; cin >> N >> M >> K;

    vector<int> modSeq(K);
    for(int i = 1; i <= 4 * N; ++i) modSeq[i % K]++;

    for(int i = 0; i < M; ++i) {
        int a, b; cin >> a >> b;
        modSeq[a % K]--; modSeq[b % K]--;
    }

    int A, B; cin >> A >> B;
    modSeq[A % K]--; modSeq[B % K]--;

    int scr = abs(A % K - B % K);

    int cnt = 0;
    int s = 0;
    for(int i = scr + 1; i < K; ++i) {
        s += modSeq[i - scr - 1];
        cnt += min(s, modSeq[i]);
        s -= min(s, modSeq[i]);
    }

    if(cnt >= M) cnt = M - 1;

    cout << cnt;
    
    return 0;
}

I번 : 통학의 신 / BOJ 17945

Tier : Bronze III
설명 보기

“근의 공식을 알고있니?” 수준의 문제다. 근의 공식으로 근을 구해서 같으면 하나만 출력, 아님 둘 다 출력하면 AC.

코드 보기 
#include <iostream>
#include <cmath>

using namespace std;

int main() {
    int A, B; cin >> A >> B;
    int x1 = (double)(-A) - sqrt(A * A  - B);
    int x2 = (double)(-A) + sqrt(A * A  - B);

    if(x1 == x2) cout << x1;
    else cout << x1 << " " << x2;

    return 0;
}

J번 : 스노우볼 / BOJ 17950

Tier : Bronze II
설명 보기

1 cm 간격으로 x배되니, 한 줄 처리할때마다 x배 시켜서 답에 더하고 출력하면 AC.

코드 보기 
#include <iostream>
#include <vector>

using namespace std;
typedef long long ll;
const ll MOD = 1e9 + 7;

int main() {
    ll H, x; cin >> H >> x;

    ll ret = 0;
    ll x_0 = x;
    for(int i = 0; i < H; ++i) {
        ll k; cin >> k;
        ret += (k % MOD) * (x % MOD);
        x *= x_0;
        ret %= MOD;
        x %= MOD;
    }

    cout << ret % MOD;
}

K번 : 디저트 / BOJ 17953

Tier : Gold V
설명 보기

2차원 DP로 해결할 수 있는 문제다. n번째 날의 최대 만족감은 n - 1번째 날의 최대 만족감에 의해 결정되기 때문에, 그렇게 부분문제로 나누어서 풀 수 있고, 이걸 점화식을 잘 만들면 \(\scriptsize O(nm ^ {2})\)에 풀 수 있다.

\(\scriptsize sat(day, type_x) = "day에 type_x를 먹었을때, 최대 만족감의 크기"\)라고 정의하자.

그러면, \(\scriptsize sat(day, type_x) = max(sat(day, type_x), value(day - 1, type_y) + sat(day - 1, type_y))\) 임을 알 수 있다. 이때 \(\scriptsize type_x = type_y\)이면 \(\scriptsize value /= 2\)해주면 된다. 이때 답은 \(\scriptsize max(sat(N, type_k))\)가 됨을 알 수 있다. 이걸 찾아서 출력하면 AC.

코드 보기 
#include <iostream>
#include <vector>
#include <algorithm>

using namespace std;

int main() {
    ios_base::sync_with_stdio(false);
    cin.tie(nullptr);
    cout.tie(nullptr);

    int N, M; cin >> N >> M;
    vector<vector<int>> dp(N, vector<int>(M));
    vector<vector<int>> seq(N, vector<int>(M));

    for(int i = 0; i < M; ++i) {
        for(int j = 0; j < N; ++j) {
            cin >> seq[j][i];
        }
    }

    for(int i = 0; i < M; ++i) dp[0][i] = seq[0][i];

    for(int i = 1; i < N; ++i) {
        for(int j = 0; j < M; ++j) {
            for(int k = 0; k < M; ++k) {
                if(j == k) dp[i][j] = max(dp[i - 1][k] + seq[i][j] / 2, dp[i][j]);
                else dp[i][j] = max(dp[i - 1][k] + seq[i][j], dp[i][j]);
            }
        }
    }

    cout << *max_element(dp[N - 1].begin(), dp[N - 1].end());

}
짧은 후기

이 셋에서 나한테 가장 개인적으로 어려웠던 문제는 아직까지도 못푼 “뜨끈한 돼지국밥“이다. 난 DP를 너무 못하는데,, 이 문젠 DP만으로 플래티넘을 찍은 문제라.. 어쩌면 지금의 나는 풀 수 없을지도 모르겠다 ㅋㅋ 가장 좋았던 문제는 투튜브라고 생각한다. 논리적인 사고만으로도 재밌게 풀 수 있던 문제라 꽤 괜찮았다고 생각한다. 윽.. 올해 대회에서 뭐라도 받을 수 있으면 좋을듯ㅎ

ACM-ICPC 2021 인터넷 예선 후기

28 Oct 2021

Internet Preliminary Contest / ACM-ICPC 2021

10월 9일 ACM-ICPC 2021 인터넷예선에 참가했다. 나(eff3ct)랑 동기님들 두분(onkkno, witoru79)님이서, 경험이나 쌓아보자라는 생각으로 새내기팀을 꾸려서 참가했다. 여튼.. UCPC에 참가할때 썼던 팀이름 그대로 Mu_Ji_Sung_-_-_-으로 참가했는데, 나중에 보니까 이름 겹치는 팀이 꽤 됐다. 아무래도 우리처럼 이름짓기가 귀찮았던게 아닐까

결론부터 말하자면 아쉽지만 본선엔 진출하지 못했다. 우리 팀은 학교 6등 전체 76등을 했당. 뭐 새내기 치곤 3솔해서 괜찮은거 아닌가 싶다는 생각이긴 하다.

2

사실 나는 4솔을 목표로 하고 나온거긴 한데, CP 경험이 많이 없어서인지 그건 역부족이었다. 우리 팀이 풀어낸 문제는 I, J, K이다.

1

I : Sport Climbing Combined (Silver 5)

스포츠 클라이밍 콤바인드 무슨 어쩌고 저쩌고 .. 사실 딱 시작하자마자 이 문제먼저 펼쳐봤다. 한분은 인쇄를 하러 나가셨구 나머지 남은 분이랑 함께 문제를 봤는데, 영어로 써져있으니 어질어질해서 무슨소리인지 도대체 잘 안들어오길래 그냥 인쇄물을 기다리고 있었다. 그래서 인쇄물이 왔을때 딱 보니, 의외로 한국어 번역페이지가 있어서 그걸 읽고 바루 std::tuple로다가 그냥 sort하고 답 찾아내고 제출했다. (12 min) 좀 늦었긴 했는데 여튼 한문제 풀고 신났었다.

J : Ten (Silver 1)

나는 다른 문제를 읽고 있었는데, onkkno님이 이거 쉬워보인다구 하시면서 문제를 푸셨다. 대충 행으로 prefix sum 찾아서 10이 되는지 찾는 방법이었던거 같은데 시간초과였나 그냥 WA였나 여튼 그게 떠서 내가 다시 문제를 보고 조금 생각을 했다. 잘 보니까 제약이 작게 걸려있어서 대충 \(\scriptsize O(n^{3})\)정도에 문제를 풀 수 있을것 같아서 그렇게 고쳐서 제출했더니 AC를 받았다. (79 min) p_ij값이 1~10만 가능하다는 점이 복잡도를 낮출 수 있다는걸 늦게 알아서 여튼 조금 늦긴 했다. 그냥 2차원 상에서 prefix sum을 sum(i, j) = 1행 1열부터 i행 j열까지 합으로 하면 \(\scriptsize O(n^{2})\) 으로 해당 테이블을 채울 수 있구. 포함배제의 원리를 활용해 각각 세그먼트들에서 합을 구한 다음 10이랑 비교하는식으로 적당히 짜주면 쉽게 풀 수 있는 문제였다. 여튼 여기까지 풀고 나니 음.. 뭔가 이제 풀 수 있는 문제가 없어보였다.

K : Treasure Hunter (Platinum 4)

보물 헌터 <- 이 문제를 푼건 조금 의외였다. 왜냐면 난 그리디 개념이 들어가는 문제들 잘 못풀어서.. ㅋㅋㅋ 머리가 셋이나 있으니 운이 좋게도 풀어진 것 같다. witoru79님이 먼저 접근법을 말해주셨는데, \(\scriptsize O(n^2)\)짜리라 TLE확정인 방법이었다. 그래서 조금 고민하다가 1시간이 슥 지나가고, 왠지 보니까 이거 보물 좌표만 보면 될 것 같네 라는 식으로 접근을해서 \(\scriptsize O(n)\)정도로 복잡도를 낮출 수 있었다. 이 때가 30분인가 40분 남겨둔 시점이었는데, 이걸 구현해보겠다구 노트북 잡고 대충 슥슥 구현해보는데, 잘 안되서 코드짜는걸 onkkno님께 넘겼다. 뇌절을 계속 하던 내 코드를 샥샥 고치시더니 야무지게 예제가 다 잘 나오는것을 확인하고 제출했다. 그리구 AC (160 min). 사실 20분 남긴 시점에서 이제 풀 수 있는 문제가 없음을 직감하고, 스코어보드 구경하다가 예선이 끝이 났다.

사실 B, E, H번도 해보려고 시도는 했었다. 특히 B번, 약간 교과서에 나올법한 문제여서 예전에 수능 수학 30번문제들에 이렇게 개수 세는 문제들이 있었다. 그래서 그 문제들 접근이 대충 경계선 좌표들만 알아내서 포함배제 비슷하게 풀어내는거라, 걍 그것처럼 풀면 되지 않을까 싶었다. 케이스가 조금 많기도 했고, 또한 구현을 하려니 극좌표계로 써야하나 뭔지 잘 모르겠어서 구현을 미루다가 결국엔 못풀었다. ㅜㅜ 푼 사람들 얘기하는거 보니 풀이가 그게 맞다고.. 여튼 젤 아쉬운 문제 ㅋㅋ 4솔했으면 본선 진출해볼수도 있었는데 까비 아깝소..

E번은 읽으면서 흠 왠지 구간으로 DP 테이블을 채우면 풀 수 있을거라 생각하긴 했는데, 딱 DP테이블 정의를 어떻게 해야할지 모르겠어서 그대로 넘겼다. ㅋㅋ solved.ac 티어는 플래티넘 3인데 dp문제는 골드5만 되어도 버거운 사람이 어캐 이걸 대회시간에 풀겠는가. 쪼금 아쉽긴 했다. 사실 DP좀 연습해보겠다고 tag:dp 해놓구 쉬운것부터 차근차근 대회전에 조금 풀었었는데, 크게 의미있진 않았다. 하루만에 DP 고수가 될 수는 당연히 없으니까 ㅎ;;ㅋ

H번두 뭔가 읽다보니 세그먼트 트리를 써서 풀면 되지 않을까 싶었는데, 이게 순서쌍이 3개짜리를 찾아야해서 그렇게 쉽진 않았다. ㅋㅋ 세그트리 좀 열심히 파둘걸 그랬나 하는 생각이 맴돈다.. 여튼 이 3문제가 대충 접근방향은 맞았는데 AC까지는 못했던 문제들이라 아쉽긴했다.

우리학교는 올해는 4솔까지 본선에 진출하게 되었다. 그래도 머 새내기팀 치고 3솔이면 잘한거아님? ㄹㅇㅋㅋ 다음해 예선엔 꼭 본선 진출할 수 있길 기원해본당. 본선 진출한 한양대팀들 파이팅~~~

[머신러닝] Linear Regression 선형 회귀 분석

20 Sep 2021

Linear Regression

고등학교 다닐때 잠시 배워보고 접었던 머신러닝을 다시 배워보려고 하고 있다. coursera.org에서 Andrew Ng 교수님의 Machine Learning 강의로 배워보는 중이다. 그때나 지금이나 이해하는 능력자체는 슬프게도 비슷한 것 같다. 여튼 2주차까지 들어보고 하니 이제 대충 Linear Regression에 대해 이해가 되는 듯 싶다.

Linear Regression, 한국어로 하자면 “선형 회귀“라는 의미이다. 말이 뭔가 어려운데, 간단하게 말해보자면 주어진 데이터셋을 가장 잘 표현할 수 있는 선형적인 함수를 찾는 문제이다.

plot

이런 데이터셋이 주어졌을때, 아래의 그림처럼 파란색의 선형적인 함수를 찾는게 바로 선형회귀인것이다.

plotrg

(데이터셋 출처 : Machine Learning - Andrew Ng 강의에서 2주차 과제)

(x는 각각의 데이터 값이고, y는 그 입력데이터 값에 대한 답, h(x)에서 도출 되는 값은 가설함수가 예측하는 모델의 값).

그럼, 이걸 어떻게 하느냐? 데이터를 표현하는 함수를 가설함수 h(x)라고 해보자. 그러면, \(\scriptsize abs(h(x) - y)\)의 합이 최소가 되는 함수 h가 곧 답이 되지 않을까? 즉, 예측값과 실제값과의 차이가 가장 적은 가설함수 모델이 가장 적합할 것이라는 소리이다. 대충 어떻게 해야 되는지 알았으니 한번 해보도록 하자. 먼저, »Linear« Regression이라는 이름에 맞게 가설함수를 \(\small h_{\theta}(x) = \theta^{T}x\)라고 하자. 이때, 세타와 x값은 열벡터로 주어진다. 세타의 transpose에 x를 곱하면 \(\scriptsize \theta_{0}x_{0} + \theta_{1}x_{1} + ...\) 같은 선형함수꼴로 나타남을 알 수 있다. x의 차원은 feature 개수를 몇개로 하느냐에 따라 달라진다. 여튼 이렇게 표현되는 가설함수를 이용해서 함수 하나를 새로 만들어보자

\[J(\theta) = \frac{1} {2m}\sum_{i=1}^{m}(h_{\theta}(x^{(i)}) - y^{(i)}) ^ {2}\]

함수 J(비용함수)를 이런식으로 한번 정의해보자. 이때, m은 데이터의 개수이다. 즉, 식의 의미는 데이터 분산의 1/2 이다. 이 J라는 함수는 가설함수가 예측한 값과 실제값이 얼마나 떨어져 있는지 잘 나타내주니(분산이 그런 의미니까) 떨어져 있는 정도가 최소가 되는 세타값들을 찾아주면 된다. 최소값을 어떻게 구하냐..? 대충 2가지 정도가 있다.

1. Gradient Descent

2. Normal Equation

Gradient Descent는 J를 편미분해 찾은 값으로 그래프의 경사를 따라 내려오며 local minimum을 찾는 알고리즘이고, Normal Equation은 그냥 \(\scriptsize J'(\theta) = 0\)이 되는 세타값을 수식으로 찾아주는 방법이다.(미분계수가 0인 지점에서 극소값을 가지기 때문임.)

후자의 Time Complexity는 \(\scriptsize O(N ^ {3})\)인 반면, Gradient Descent는 잘만 만들어주면 그것보단 빠르게 값을 찾을 수 있다. 즉, 데이터 크기가 작을때는 그냥 Normal Equation으로 값을 구하되, 크기가 커지면 Gradient Descent를 이용해서 찾아주면 되는 것이다.

먼저 Gradient Descent를 간단하게 알아보자. 그래프에서 가파른 부분을 따라 내려가주면 local minimum을 찾을 수 있다는 것은 자명하다. 그렇기 때문에 \(\scriptsize \theta := \theta - \alpha \cdot J'(theta)\)를 해주면 되지 않을까? \(\small \alpha\)의 값은 빠르게 수렴할 수 있는 크기로 설정해주면 된다. 아래는 위 식을 풀어서 정리한 식이다. 알파와 m을 제외한 모든값은 벡터라고 생각하면 된다.

\[\theta := \theta - X^{T}(X \theta - y) \cdot (\frac{\alpha}{m})\]

이 과정을 여러번 해주면 결국엔 Local Minimum으로 수렴하게 되고, 우리가 원하는 세타값을 찾을 수 있게 된다. 근데, 이 알고리즘 말은 쉽지만, 사실 해줘야할게 좀 많다. Learning Rate라고 불리는 \(\small \alpha\)값도 설정해주어야하고, 수렴하는지 여부도 체크해줘야한다. 또한, 각각의 feature가 극단적인 scale을 가진다면(x1이 (-1, 1)인데 x2가 (-10000000, 10000000) 이런식인 경우) feature scaling을 통해 범위를 맞춰야만 하는 번거로움이 있다. 그래서 데이터 수가 적을때는 Normal Equation을 사용하는 쪽이 더 간편하다.

Normal Equation은 식을 이러쿵 저러쿵 조작해서 J’이 0이 되는 theta를 직빵으로 얻어낼 수 있는 방법이다. 아래의 식으로 해결할 수 있다.

\[\theta = (X^{T}X) ^ {-1} X^{T}y\]

이게 Inverse를 계산하는데 \(\scriptsize O(N ^ {3})\) cost가 소요되어서 느리긴 하지만, 저 식만 써주면 그냥 바로 찾아낼 수 있는 간편함을 보여준다.

이런 두 방법으로 J가 최소가 되는 세타를 찾을 수 있다. 그런데.. 선형함수말고는 못하는걸까? 사실 그런것도 아니다.. 당연히 가능하다. 단지 비선형으로 나타내어진 h를 선형으로 고치기만 하면 위 내용을 그대로 적용할 수 있기에, 문제될 것도 없다. 즉, \(\scriptsize h(x) = \theta_{0} + \theta_{1}x_{1} + \theta_{2}x_{2}^{2}\) 처럼 주어지면, 새로운 변수 \(\scriptsize x'_{2} = x_{2}^{2}\)라고 하면 그만이다. 그냥 비선형적인 요소들을 모조리 바꿔주면 Linear Regression을 적용시킬 수 있다.

여튼 최근에 이런 내용들을 배워보고 있다. 아직까진 재밌는 것 같은데.. 점점 수식이 뜬금없이 툭툭하고 튀어나오니 슬슬 어지러워지기 시작하고 있다. 수학을 그닥 잘하는 편이 아닌지라,, 올해 안에 과연 제대로 다 배울 수 있을까?

[백준 BOJ] 2252. 줄 세우기

09 Sep 2021

난이도

Gold II

문제 풀이

그냥 위상정렬의 결과를 출력하면 되는 문제이다. 주어지는 학생들의 번호를 하나의 노드라고 생각하면, 번호들의 순서가 곧 노드가 연결되는 순서이다. 그 순서를 알고 싶은 것이니, 위상정렬을 수행해 답을 구해내면 된다. 시간 복잡도는 위상정렬의 시간복잡도인 \(\scriptsize O(V + E)\)이다. (V는 노드 개수, E는 간선 개수) 하여튼 그냥 위상 정렬을 그대로 구현하면 된다. 위상정렬에 대한 자세한 설명

void topologySort(vector<vector<int>>& adj, vector<int>& count) {
    vector<int> ret;
    queue<int> q;
    for(int i = 1; i <= N; ++i) {
        if(count[i] == 0) q.push(i);
    }

    for(int i = 0; i < N; ++i) {
        int now = q.front();
        q.pop();

        ret.push_back(now);
        
        for(int j = 0; j < (int)adj[now].size(); ++j) {
            if(--count[adj[now][j]] == 0) q.push(adj[now][j]);
        }
    }

    for(auto& element : ret) cout << element << ' ';
}

요렇게 위상정렬을 써주고 출력하면, AC를 받을 수 있다.

코드 전문

2252 // 줄 세우기

[알고리즘 Algorithm] 위상정렬(Topology Sort)

09 Sep 2021

위상 정렬(Topology Sort)

위상정렬은 노드간 위상에 따라 노드들의 순서를 정하는 정렬방법이다. 무슨 소리인지는 아래의 그림으로 알아보자

sort

그래프를 보면, 크게 1 2 3 5와 4 3의 순서를 가지는 것을 알 수 있다. 이를 순서대로 표시하면, 위 sort에 표시한 순서들 중 하나로 표시할 수 있겠다. 즉, 위상정렬은 간단하게 말하자면, 어떤 DAG(Directed Acycle Graph, 유향 무사이클 그래프)에서 노드의 순서를 찾는 방법이다. 당연하게도 무향 그래프이거나, 사이클이 있으면 위상으로 정렬하기 어렵기에 위상정렬은 DAG에 한정된다.

이런것을 어디에 쓰냐면, 순서를 지켜서 관계를 이루어야만 하는 문제들에 쓰인다. BOJ의 2252 줄세우기 같은 문제를 이런 위상정렬을 사용해 풀어낼 수 있다. (->2252번 풀이보기) 위상정렬은 큐를 활용해서 구현할 수도 있고, 스택을 활용해서 구현할 수도 있다. 여기에서는 간단하게 큐를 사용해서 푸는 방법을 알아보자.

1. 어떤 노드 X가 있을때, 그 노드로 연결되는 간선이 없는 노드들을 큐에 push한다.

2. 큐에서 노드를 꺼내 정렬됐음을 표시하고, 그 노드와 연결되어 있는 다른 노드들과의 간선을 끊어준다.

3. 연결되어 있었던 다른노드들 중에서 연결되는 간선이 없는 노드를 찾아 큐에 push한다.

4. 2번 ~ 3번 과정을 노드수만큼 반복한다.

이 과정을 따라가면, 위상순으로 정렬된 노드들을 얻을 수 있다. 그림으로 알아보자.

l

아무것도 연결되지 않은 1과 4를 queue에 push한다. (1번 과정)

2

queue에서 1을 꺼내 연결된 간선을 지워주고 아무것도 연결되지 않은 노드인지 검사해 queue에 push한다. 이 경우에는 2가 아무것도 연결되지 않은 노드가 되므로 2를 queue에 push한다. 그 다음, 4를 꺼내 마찬가지의 과정을 진행해주면 위 그림처럼 된다.

3

4

같은 과정을 이렇게 반복해 주면, queue가 모두 비는 시점에 ret에 topology sort의 결과가 저장된다.

이렇게 짜기 위해서는 연결되어 있는 노드 수가 몇개인지 알고 있어야 하기에 그래프를 입력받을때 아래의 코드처럼 따로 해당 노드에 연결되어 있는 개수를 세어주어야한다.

//N은 노드의 개수, M은 간선의 수
vector<vector<int>> adj(N + 1, vector<int>()); //인접 리스트
vector<int> count(N + 1, 0); //노드에 몇개가 연결되어 있는지

for(int i = 0; i < M; ++i) {
    int u, v; cin >> u >> v;
    adj[u].push_back(v); //u -> v로 연결되는 간선
    count[v]++; //v노드에 u 하나가 연결되어있는 것이니 +1 해준다.
}

이렇게 데이터를 받아주고 나면 위상정렬을 할 준비가 완료된 것이다. 그냥 위의 과정을 그대로 코드로 구현하면 되기에 아래와 같이 짜줄 수 있다.

void topologySort(vector<vector<int>>& adj, vector<int>& count) { //인접리스트와 연결된 노드수를 파라미터로 받는다
    vector<int> ret; //결과를 저장할 벡터
    queue<int> q; 
    for(int i = 1; i <= N; ++i) {
        if(count[i] == 0) q.push(i); //연결된 개수가 0개이면 queue에 push
    }

    for(int i = 0; i < N; ++i) { //노드 수만큼 반복해주면 된다.
        int now = q.front(); //queue에서 원소를 꺼내고 pop한다.
        q.pop();

        ret.push_back(now); //그 원소는 ret에 push한다.
        
        for(auto& next : adj[now]) { 
            if(--count[next] == 0) q.push(next); //간선을 지우고(count 감소 시키는걸로 충분하다.) 그 값이 0이면 queue에 push
        }
    }

    for(auto& element : ret) cout << element << ' '; //출력
}

BOJ에서 위상정렬을 활용해 풀만한 문제는 위에서 소개한 2252 줄세우기와 1005 ACM Craft정도가 있을 듯 하다. 전자는 그냥 위상 정렬 그 자체로 풀 수 있고, 후자는 위상정렬 + 간단한 DP로 풀 수 있다. 나는 후자가 더 어렵다고 생각하는데.. 왜인진 모르겠으나 티어는 전자가 더 높다. 여튼, BFS나 DFS로만은 해결할 수 없는 그런 문제들을 해결할 수 있는 그래프 분석 도구이다. 구현하기 복잡하지 않고 쉽기 때문에, 알아두면 좋을 듯 하다.