18 Jul 2022
난이도
Platinum IV
문제 풀이
작년 인예때는 세그 트리 문제인것만 직감하고 못풀었는데, 이제 풀 실력이 만들어졌다. 새벽에 야무지게 풀고 신나서 풀이 쓰는 중이다.. 하여튼 대충 정렬 + 약간의 DP(?) + 세그먼트 트리로 풀 수 있는 문제이다.
문제에서 구해야하는 것은 두 수열이 주어졌을 때, 오름차순을 만들 수 있는 인덱스 쌍 \(\scriptsize (i, j, k)\)의 개수를 찾는 것이다. 일단, \(\scriptsize i, j, k\) 모두가 변하면 어질어질하니 \(\scriptsize p, q\)를 묶어서 정렬해주자.
std::pair를 이용해서 정렬해주면, first에 담긴 쪽은 오름차순이 된다. 이제 second를 보고 순서쌍 개수를 세어주면 되는데, 내가 생각한 방법은 다음과 같다. 먼저, 배열 하나를 정의해보자.
\(cnt(i) :=\) “i로 끝나는 2자리 증가수열의 개수”
이렇게 \(\scriptsize cnt\)를 정의하면, 2개짜리 증가 순서쌍은 찾을 수 있다.
\[cnt(i) = \sum_{j < i \land q[j] < q[i]} 1\]
naive하게 계산하면 \(\scriptsize O(n^{2})\)이지만, 세그먼트 트리로 최적화해줄 수 있으니 \(\scriptsize O(nlogn)\) 만에 배열을 채울 수 있다.
segment_tree tree(MAX + 1);
vector<ll> cnt(n + 1);
for(int i = 1; i <= n; ++i) {
cnt[i] = tree.query(0, MAX, 1, 0, X[i].second - 1);
tree.update(0, MAX, 1, X[i].second, 1);
}
cnt 배열은 \(\scriptsize i < j\) 인 쌍의 개수를 센거니까 이제 \(\scriptsize i < j < k\) 개수를 세어보자. \(\scriptsize cnt\)를 채우는 것과 비슷하게 개수를 세줄 수 있다. 요것도 역시 세그먼트 트리로 샤샥 해주면 된다.
\[\sum_{j < i \land q[j] < q[i]} cnt[j]\]
ll ans = 0;
segment_tree tree_cnt(MAX + 1);
for(int i = 1; i <= n; ++i) {
ans += tree_cnt.query(0, MAX, 1, 0, X[i].second - 1);
tree_cnt.update(0, MAX, 1, X[i].second, cnt[i]);
}
현재보고 있는 원소보다 작은 원소들의 \(\scriptsize cnt\)값을 다 더하면 그게 우리가 찾는 값이니까 반복문을 돌면서 답에 더해주면 된다. 이렇게 하면 답이 잘 안나온다. 왜냐면, 중복된 원소에 대해서 값을 잘못 세기 때문이다. \(\scriptsize p\)값이 같을 때에는 \(\scriptsize q\)값이 큰 걸 먼저 앞에 둬야지 값을 제대로 셀 수 있다. 정렬을 똑바로 하고 답 출력해주면 AC!
1-based로 코드를 썼는데, 그러다가 sort 시작을 begin + 1이 아닌 begin으로 해버려서 맞왜틀 좀 했었다.. 혹시 너무 맞는거 같은데 틀린다면 이게 원인일 수 있다.
코드 전문
23245 // Similarity
17 Jul 2022
난이도
Silver III (이지만.. 이보다 더 높다고 생각함)
문제 풀이
이거 내가 풀 때는 브론즈1이 박혀 있던 어마어마한 문제였다.
동아리 학술부장님이 브론즈가 안풀린다길래 보러 갔는데, 나도 바로 안풀려서 진짜 당황했다. 문제를 간단하게 요약하자면, 삼각형으로 정이십오각형을 덮어서 모든 간선을 덮는 문제다. 모든 간선을 덮을 수 있는 삼각형을 출력해주면 되는데, 총 300개의 간선을 100개의 삼각형으로 덮으면 된다.
각 간선이 쓰여지지 않은 것만 골라서 삼각형을 만드는 방법으로 접근을 해봤는데, 그렇게 하면 80개정도만 덮인다. 그래서 조금 야매로.. 삼각형 몇개를 이미 만들었으면 좀 조건을 완화해서 삼각형을 만들도록 해봤는데, 젤 많이 줄인 횟수가 128개였다. 128개로 300개를 다 덮을 수 있었는데, 문제에서 요구하는건 아쉽지만 100개 ^^..
오~ 도대체 어떻게 푸는걸까?
대충 이쯤에서 브론즈1일리가 없다는 생각이 강하게 들었다. 그래서 문제 출처를 찾아서 본 대회 스코어보드를 봤는데, 푼 팀이 5팀밖에 없었다. 군인(진)분께서 풀이 설명하신걸 보고 그제서야 풀 수 있었는데, 삼각형 변의 길이를 unique하게 만들어버리면 됐었다.
삼각형의 변을 모두 다 다르게 구성해보자. 꼭짓점 하나를 건너뛰면 1만큼의 변이 만들어졌다고 생각하고, 비슷하게 두 개를 건너뛰면 2만큼의 변이 생겼다고 생각할 수 있다. 꼭짓점을 몇 개만큼 건너뛰냐에 따라 변의 길이가 달라지는 것이다! 진짜 발상 한 번 어렵다. 하여튼 이 삼각형을 돌리면서 출력해주면, (1, 2, 3)에 대한 간선들은 모두 덮이는 것이다.
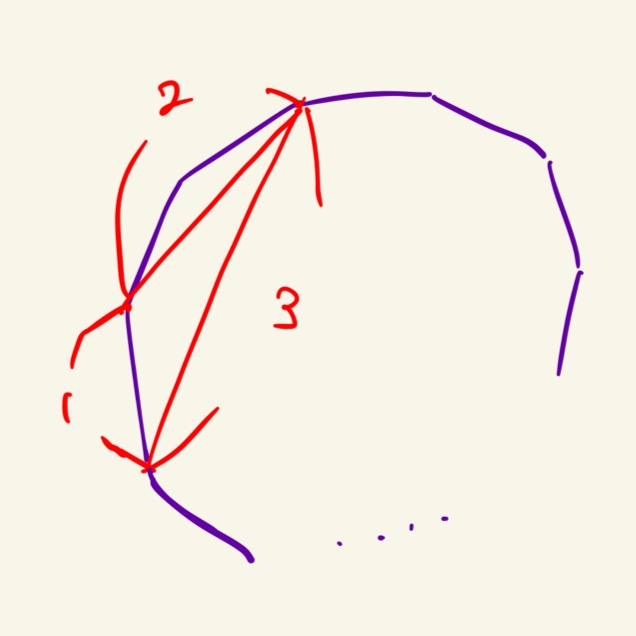
문제에서는 정이십오각형일 때를 구하라고 한다. 그럼.. 1 ~ 12까지의 간선이 생길걸 예상할 수 있는데, 각 변이 unique한 삼각형이 몇개가 필요할까?
삼각형 하나 당 간선 3개를 커버할 수 있다. 1 ~ 12까지 모든 수가 나오게 하려면 삼각형 4개가 필요하다는 걸 알 수 있다. 공교롭게도 25 * 4 = 100이니 그 삼각형들을 찾으면 문제 정답을 맞출 수 있다.
생각없이 수를 쓰니까 해를 찾았는데, 내가 찾은 해는 \(\scriptsize (1, 2, 3), (4, 7, 11), (5, 8, 12), (6, 9, 10)\) 이다. 그냥 진짜 숫자 몇개 쓰다가 우연히 찾았다. 완전탐색으로 잘~~ 하면 찾을 수 있을 것 같긴 한데.. 여튼 이렇게 모든 수가 다 나오는 삼각형들을 찾아서 이걸 25번 돌리며 출력해주면 된다.
#include <bits/stdc++.h>
using namespace std;
using ll = long long;
using pii = pair<int, int>;
using ppii = pair<int, pii>;
int main() {
ios_base::sync_with_stdio(false);
cin.tie(nullptr);
cout.tie(nullptr);
for(int i = 0; i < 25; ++i) {
int a = i % 25, b = (i + 1) % 25, c = (i + 3) % 25;
int d = (i + 4) % 25, e = (i + 11) % 25;
int f = (i + 5) % 25, g = (i + 13) % 25;
int h = (i + 6) % 25, j = (i + 15) % 25;
cout << char('A' + a) << char('A' + b) << char('A' + c) << '\n';
cout << char('A' + a) << char('A' + d) << char('A' + e) << '\n';
cout << char('A' + a) << char('A' + f) << char('A' + g) << '\n';
cout << char('A' + a) << char('A' + h) << char('A' + j) << '\n';
}
return 0;
}
코드 진짜 무지성으로 짰다. ㅋㅋ
풀고나서 브론즈1은 절대 말도 안된다고 생각해서 소신대로 골드5에 기여하고 몇 분뒤에 보니, 이미 기여하신분도 의견을 바꿔서 하루만에 티어가 3개나 오른(…) 문제가 되어버렸다.
코드 전문
21042 // Triangle of Safety
12 Jul 2022
난이도
Platinum IV
문제 풀이
\(\scriptsize N\)개의 도시에 \(\scriptsize N - 1\)개의 도로가 있고, 어느 두 도시를 골라도 해당 도시를 잇는 경로가 존재한다는 점에서 그래프가 트리로 고정된다.
\(\scriptsize K\)개의 쿼리가 주어지고, 각 쿼리는 두 노드를 연결하는 경로 위에 존재하는 엣지들 중, 가장 짧은 것과 가장 긴 것을 찾는 것이라 생각할 수 있다.
Naive하게 생각하면, 쿼리가 주어질 때마다 경로를 전부 탐색해주면 된다. 이 방법으로 문제를 해결할 경우 쿼리 당 \(\scriptsize O(N)\)이다. 그러나, 아쉽게도 총 시간복잡도가 \(\scriptsize O(KN)\)이니 시간초과를 받는다. 그러면, 쿼리 당 \(\scriptsize O(N)\)보다 빠르게 처리해야 한다는 의미이다. \(\scriptsize O(log N)\) LCA와 희소 배열을 사용하면, 쿼리 당 \(\scriptsize O(log N)\)으로 처리할 수 있다.
\(f(i, j) :=\) “\(i\)번 노드에서 \(2^{j}\)번 루트 쪽으로 이동할 때, 찾을 수 있는 가장 짧은 도로의 길이”
\(parent(i, j) :=\) “\(i\)번 노드의 \(2^{j}\)번째 부모 노드”
라고 정의하자. \(\scriptsize 2^{j} = 2^{j - 1} + 2^{j - 1}\) 라는 점을 생각하면 다음 같은 관계식을 유도할 수 있다.
\[f(i, j) = \min(f( parent(i, j - 1), j - 1), f(i, j - 1))\]
\(\scriptsize 2^{j - 1}\)번째까지 최솟값과 \(\scriptsize 2^{j - 1}\)번째부터 \(\scriptsize 2^{j}\)까지의 최솟값을 비교해서 작은 값이 \(\scriptsize f(i, j)\)이 되기 때문이다. 이 논리를 가장 긴 도로의 길이를 구하는데에도 그대로 적용시킬 수 있다. 이를 미리 전처리 해두면 공간복잡도 \(\scriptsize O(NlogN)\), 전처리 하는데 시간복잡도 \(\scriptsize O(NlogN)\) 이고 LCA를 활용해 쿼리 당 \(\scriptsize O(log N)\)에 처리 가능하다. 따라서 총 시간복잡도 \(\scriptsize O(NlogN + KlogN)\)에 해결 가능하다.
for(int j = 0; j < sz; ++j) {
for(int i = 1; i <= N; ++i) {
if(parent[i][j] == -1) continue;
parent[i][j + 1] = parent[ parent[i][j] ][j];
max_dist[i][j + 1] = max(max_dist[i][j], max_dist[ parent[i][j] ][j]);
min_dist[i][j + 1] = min(min_dist[i][j], min_dist[ parent[i][j] ][j]);
}
}
dfs를 이용해 \(\scriptsize j = 2^{0}\)에 대한 값을 모두 채워준 후, 위 코드처럼 배열들을 전처리해주고 LCA를 잘 이용해서 답을 구해주면 된다.
코드 전문
3176 // 도로 네트워크
10 Jul 2022
난이도
Diamond V
문제 풀이
요약하자면, 넓이가 \(\scriptsize S\)인 서로 다른 평행사변형들의 개수를 찾는 문제다. 문제를 처음보고 떠올린 풀이는 벡터를 여러개 만들어서 서로 외적시킨 다음, 외적의 크기로 어찌저찌 값을 구할 수 있지 않을까.. 였다. 뇌절 그 자체였다. \(\scriptsize O(NlogN)\) 개 정도의 벡터가 필요하지 않을까.. 생각하다가 조화급수부터해서 뇌절이 거듭되길래 도저히 말이 안되는 풀이같아서 그냥 자러갔다. (오후 1시에 자는 낮밤이 뒤바뀐 삶.. ㅋㅋ;;)
여튼, 자고 일어나서 다시 생각해서 도형을 직접 그려서 구하는걸 그려봤다.
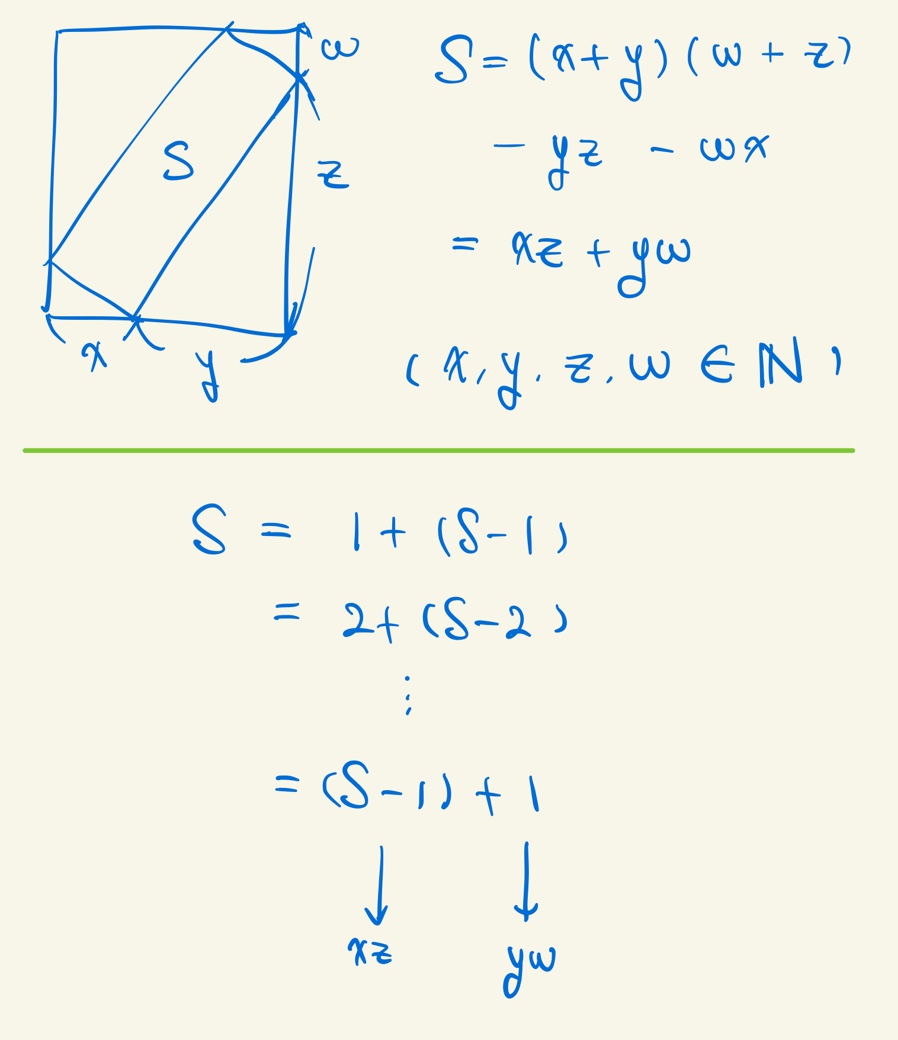
그림처럼 자연수 곱의 합으로 S를 표현할 수 있다. 두 자연수를 곱해서 \(\scriptsize k\)가 되는 경우의 수를 \(\scriptsize A_{k}\)라고 해보자. \(\scriptsize k = 1\)부터 \(\scriptsize k = S - 1\)까지 \(\scriptsize A_{k}A_{S-k}\)를 다 더해주면 그 값이 \(\scriptsize S\)일 때 평행사변형의 개수가 된다.

문제를 풀기 위해서는 \(\scriptsize S = 1\)부터 \(\scriptsize S = 500000\)까지 값이 필요하다. 따라서, \(\scriptsize A\)를 해당 범위까지 잘 구한 다음 convolution 해주면, 원하는 값을 얻을 수 있다.
\(\scriptsize n = 500\)이고, 쿼리 구간이 최대 \(\scriptsize 500000\)이라 쿼리 하나 처리하는데 \(\scriptsize O(N)\)이어서 TLE 날 것 같지만.. 의외로(?) 안난다. 세그먼트 트리 짜기가 귀찮아서 15초의 믿음을 가지고 제출했는데, 별 다른 최적화 없이도 500ms 부근으로 AC를 받을 수 있다. 총 시간 복잡도는 \(\scriptsize O(QN + NlogN)\)이다 (Q는 쿼리 개수, N은 500,000).
코드 전문
10793 // Tile Cutting
05 Jul 2022
난이도
Diamond V
문제 풀이
요약하자면, 단순히 inversion을 찾는 문제다. 그런데, 임의의 길이 K에 대해 K만큼 간격을 두고 떨어져있는 inversion 쌍들의 개수를 모두 세어 모두 출력해줘야하는 문제다.
요구하는건 분명 쉬운데.. 모든 길이의 inversion 쌍들을 다 찾아야 하는 점에서 문제가 어려워진다.
문제를 풀기 위해 주어진 걸 어떻게든 수식으로 바꿔보려 시도해보자. 먼저, B가 먼저 나오고 A가 나중에 나와야 inversion인 것은 자명하다. 다소 뜬금없지만, 이 성질을 이용해 아래 그림처럼 생각해 볼 수 있다.
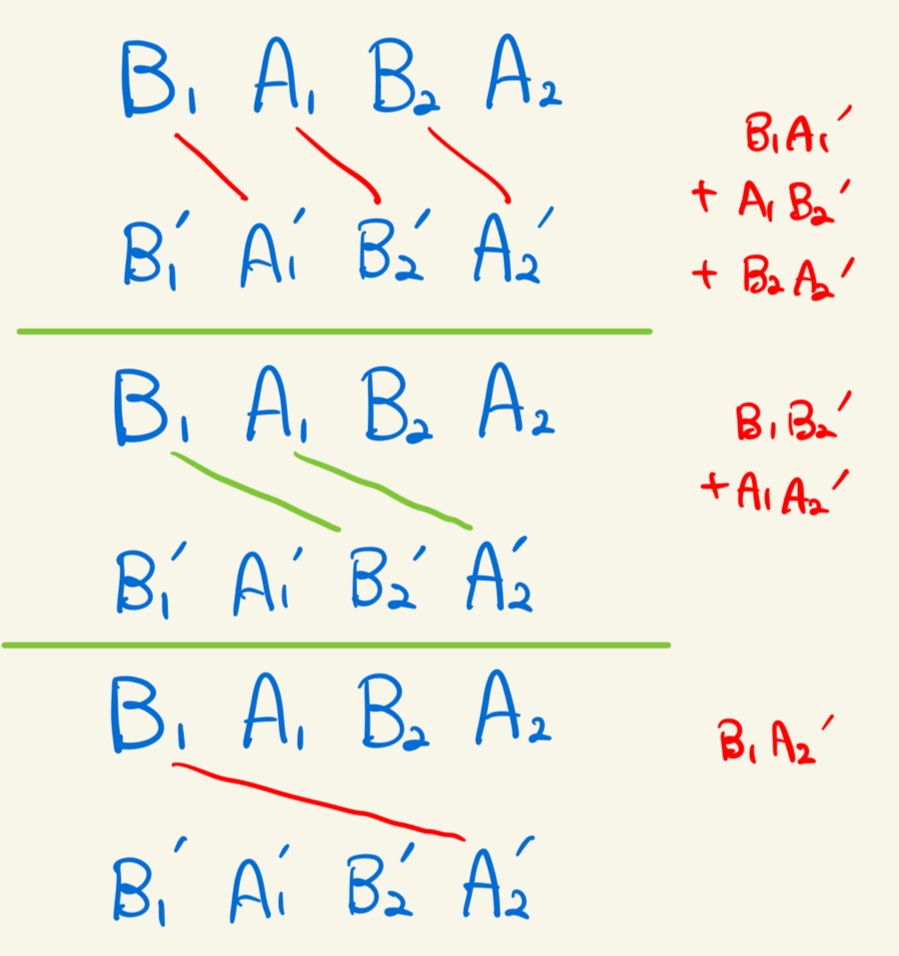
주어지는 스트링을 위 아래로 각각 두고, 위쪽은 \(\scriptsize B = 1, A = 0\)이라 하고 아래쪽은 \(\scriptsize B' = 0, A' = 1\)이라고 하자. 그럼 각 길이의 inversion 개수를 그림에 적힌 수식으로 전개할 수 있다. 그럼 저 값들을 찾아내는 것으로 문제가 변하는 데 Naive하게 생각하면 \(\scriptsize O(N^{2})\)임이 자명하고, 그렇게 풀면 TLE을 받는다.
따라서, \(\scriptsize O(N^{2})\)보다 빠른 풀이를 가져와야 한다.
식의 형태를 잘 관찰하고 있으면, convolution 꼴로 왠지 고칠 수 있을 것 같다(라는 느낌이 들어야하는 듯..).
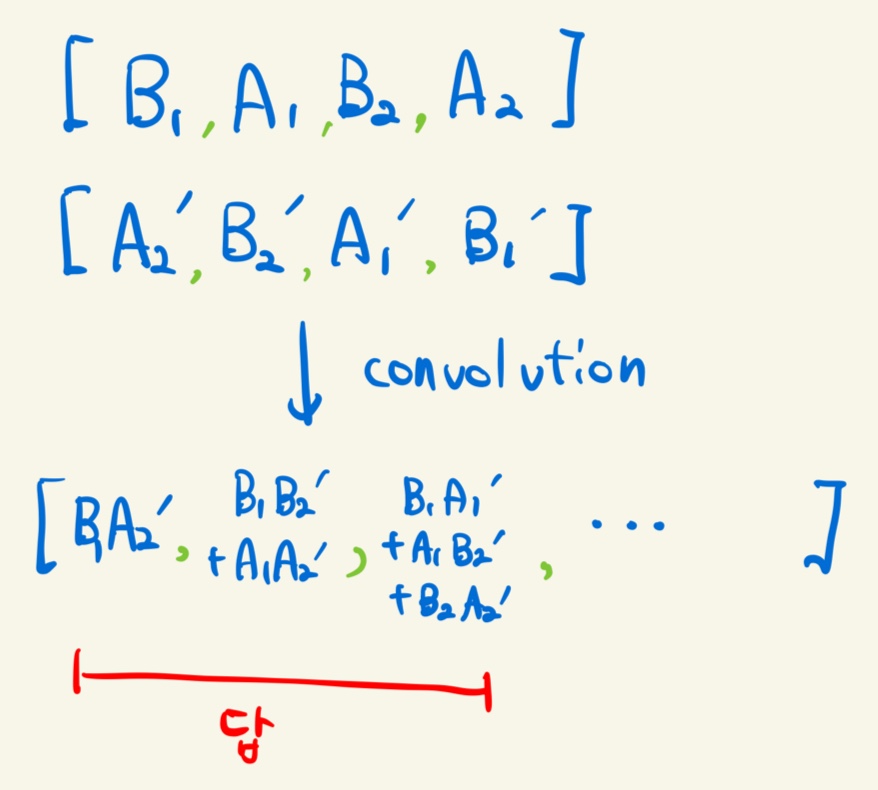
아래 스트링을 뒤집고 위 아래를 convolution한 결과를 보면 고맙게도 우리가 찾는 값들이 역순으로 저장되서 나온다는 사실을 알 수 있다. 이렇게 \(\scriptsize 0\) ~ \(\scriptsize N - 2\)번째 까지 계수를 역순으로 출력해주면 그게 정답이다. 이렇게 풀면, \(\scriptsize O(NlogN)\)에 문제 해결이 가능하다.
문제를 풀면서 느끼는건데.. FFT 문제들은 조금 뜬금없는 모델링을 필요로 한다는 느낌이다.
코드 전문
13055 // K-inversions




