17 Aug 2021
난이도
Gold I
문제 풀이
제곱 ㄴㄴ수를 찾는게 쉬울까 아니면 제곱수로 나누어지는 수들을 찾는게 쉬울까? 전자는 그 수보다 작은 제곱수들로 모두 나누어봐야 알 수 있겠지만, 후자는 제곱수의 배수들만 찾아주면 된다. 따라서 후자가 더 쉽다는 판단하에 문제를 풀었다. 이 문제를 풀기 위해 제곱수들로 나누어지는 수들을 모두 찾아내면 되는데, 이 과정이 소수들을 찾을 때 에라토스테네스의 체(Eratosthenes’s Sieve)를 사용하는것과 유사하다. 즉, 나는 에라토스테네스의 체를 살짝 변형해 제곱수의 배수들을 지워나가는 식으로 체를 만들면 된다고 생각했다.
이 문제 잘 보면, max값이 \(\small 10^{12} + 10^{6}\)까지 주어질 수 있다. 그렇기에, 소수들을 찾을때처럼 bool 배열을 \(\small 10^{12} + 10^{6}\) 만큼의 크기로 만들게 된다면, 당연히 메모리 초과가 일어난다. 우리가 필요한건 min과 max사이에 몇개의 제곱 ㄴㄴ수가 있는지 궁금하니 \(\small max - min + 1\)개 만큼만 정보가 필요하다는 것을 알 수 있다. 그래서 최대 \(\small 10^{6} + 1\) 크기의 배열로 문제를 해결할 수 있도록 하면 된다. 단순히, min부터 인덱스를 0으로 생각하고 풀면 된다는 소리이다. 구현을 한다면 아래의 코드처럼 할 수 있다.
void solve(ll m, ll M) { //m == min, M == max
vector<bool> isJegopNoNo(M - m + 1, true);
for(ll i = 2; i <= sqrt(M); ++i) {
ll k = ceil(double(m) / double(i * i));
for(ll j = (i * i) * k; j <= M; j += (i * i)) {
isJegopNoNo[j - m] = false;
}
}
int ret = 0;
for(int i = 0; i < isJegopNoNo.size(); ++i) {
if(isJegopNoNo[i]) ret++;
}
cout << ret;
}
이때, ll은 long long이다 (int형 범위를 넘어가기 때문에 int보다 큰 자료형으로 해주어야 overflow가 일어나지 않는다.).
바깥쪽 루프를 보면 \(\small \sqrt{M}\)까지만 돌게 되는데, \(\small \sqrt{M}\)보다 큰 수를 제곱하면 M보다 커지기 때문에 검사해줄 필요가 없기 때문이다. 어떤 제곱수 \(\small i^{2}\)의 배수가 min값 보다 클 때, 숫자들을 지워야 하는데, 이를 위해서 간단한 부등식을 생각해보자. \(\small i^{2} \cdot k \geq min\) 인데, 이를 만족하는 k의 최소값이 \(\left \lceil \frac {m}{i^{2}} \right \rceil\) 이다. 따라서 저 값부터 시작해 \(\small i^{2}\)을 더해주며 배수를 지우면 된다.
모든 제곱수의 배수를 지우고 나서 남은 수들이 제곱 ㄴㄴ수임이 자명하므로, 그 수들의 개수를 세어 출력해주면 끝이다.
나는 처음에 예상치 못한 에러로 디버깅을 조금 했는데, 그 이유는 바깥쪽 루프에 초기값을 long long이 아닌 int로 해놨었기 때문에 오버플로우가 났었다. \(\small \sqrt{M}\)값이 int범위라는것만 생각하고 있었기에 제곱에 대해서 전혀 고려를 안했는데, 이를 깨닫고 long long로 고치니 해결됐다… 이런 어처구니 없는 실수를 조심하도록 하자..
코드 전문
1016 // 제곱 ㄴㄴ 수
10 Aug 2021
난이도
Silver I
문제 풀이
테스트 케이스에 대해 골드바흐의 추측을 검증하는 문제이다. 그래서 주어지는 짝수 정수 n보다 작은 소수들을 모두 다 알아야할 필요가 있다. n의 최대값은 1,000,000이니, 백만까지의 소수들을 구하자.
소수들을 구하는데에는 ‘에라토스테네스의 체(Eratosthenes’s Seive)’라는 알고리즘이 사용된다. 에라토스테네스의 체는 n이하의 수들에서 소수를 얻어내는데 사용되는데, 아이디어는 간단하다. 먼저 가장 작은 소수인 2부터 시작해서 그 배수들을 전부 다 지워낸다. 모든 배수를 다 지워냈으면, 그 다음으로 작은 소수를 택해 그 소수의 배수들을 모두 지운다. 이렇게 계속 반복하면 남는것은 필연적으로 소수이게 된다. 이를 코드로 짜면 다음과 같다.
//eratosthenes's sieve
isPrime[0] = isPrime[1] = false;
for(int i = 2; i <= 1000; ++i) {
if(isPrime[i]) {
for(int j = i * i; j <= 1000000; j += i) {
isPrime[j] = false;
}
}
}
isPrime이라는 bool형 배열을 만들고, 그 배열에 소수인지 아닌지를 표시한다.(기본 설정값은 모두 true)
0과 1은 소수가 아니므로 제외해주고 2부터 시작해서 배수들을 지워준다. 이때 \(\small \sqrt{n}\)까지만 이 과정을 수행해도 모든 소수를 구할 수 있다. 따라서, \(\small\sqrt{n} = 1000\) 까지만 반복문을 돌고, 그 배수들을 지워준다. 이때, 안쪽 루프는 \(\small i^{2}\)부터 시작하는데, 그 이유는 \(\small (i - 1) \cdot i\)처럼 \(\small i^{2}\)보다 작은 배수들은 이전에 이미 지워지기 때문이다. 그래서 \(\small i^{2}\)부터 돌도록 최적화해줄 수 있다. 이렇게 코드를 짜면, 시간복잡도는 \(\small O(nlog(logn))\)이라고 한다. \(\small log(logn)\)이 굉장히 느리게 증가하기 때문에 사실상(n이 매우매우 큰수가 아니면) \(\small O(n)\)과 거의 같은 시간복잡도이다.
//save prime numbers
vector<int> primeVector;
for(int i = 3; i <= 1000000; ++i) {
if(isPrime[i]) primeVector.push_back(i);
}
그렇게 소수들을 찾고 그 소수들을 primeVector에 모두 넣어주었다. (이때, 2는 제외하도록 한다.)
소수들을 찾았으면, 그 소수들로 어떻게 해야 b - a가 최대가 되면서 n = a + b꼴로 출력할 수 있는지 생각해보아야 한다.
가장 간단한 방법은 n보다 작은 모든 소수들을 돌아보며 a + b = n이 되는지 체크하고 b - a가 최대가 되는 때를 저장하는것이다.
void solve(int& n, vector<int>& primeVector) {
int a = 0, b = 0;
int lb = lower_bound(primeVector.begin(), primeVector.end(), n) - primeVector.begin();
for(int i = 0; i < lb; ++i) {
for(int j = i; j < lb; ++j) {
if((primeVector[i] + primeVector[j] == n) && (primeVector[j] - primeVector[i]) >= (b - a)) {
a = primeVector[i];
b = primeVector[j];
}
}
}
cout << n << " = " << a << " + " << b << '\n';
}
이렇게 짜면, 분명 숫자는 찾아진다. 그러나, \(\small O(n^{2})\)이라 TLE를 받게된다. 백만까지의 소수 개수는 78000개 정도이다. 그래서 TLE를 받게 된다. 그렇다면 \(\small O(n^{2})\)보다 작은 복잡도를 가지는 방법을 생각해보아야한다. n보다 작은 소수들 중 가장 큰 소수와 가장 작은 소수부터 시작해서 범위를 줄여가며 체크를 하면 되지 않을까? a b c d e(오름차순) 이 n보다 작은 소수들이라고 해보자. 먼저 a + e부터 시작한다. a + e > n이면 e를 줄이면 되니 e보다 작은 d로 체크를 해주면 된다. 만약 a + e < n이면 a를 크게해주면 되니 a보다 큰 b로 체크를 해주면 된다. 이걸 반복해 n이 되면 그때가 차이가 최대인 소수들이 될거니 분명 위의 \(\small O(n^{2})\)방법보다는 빠르게 될 것이다. 아래는 이 방법을 구현해본 것이다.
void solve(int& n, vector<int>& primeVector) {
int lb = lower_bound(primeVector.begin(), primeVector.end(), n) - primeVector.begin() - 1;
int a = 0, b = lb;
int nowSum = 0;
while(true) {
nowSum = primeVector[a] + primeVector[b];
if(nowSum == n) break;
else if(nowSum > n) b--;
else if(nowSum < n) {
a++;
b = lb;
}
}
cout << n << " = " << primeVector[a] << " + " << primeVector[b] << '\n';
}
근데, 이것보다 더 좋은 방법이 있다. primeVector[a] + primeVector[b] == n인지 체크하는 방법 대신 primeVector[b] == n - primeVector[a]임을 이용해보자. n에서 primeVector[a]값을 뺀 값이 소수라면 그게 primeVector[b]가 되지 않겠는가? 그래서, 그걸 이용하면 상당히 간단하게 코드를 짤 수 있다.
void solve(int& n, vector<int>& primeVector) {
int a = 0;
while(true) {
if(isPrime[n - primeVector[a]]) break;
a++;
}
cout << n << " = " << primeVector[a] << " + " << n - primeVector[a] << '\n';
}
n = a + b에서 a가 결정되면 b가 결정될테니, 그것을 이용해 이렇게 짜면 자연스럽게 b - a가 최대인 쌍들이 구해진다.
식을 살짝만 변형해 구하는걸 바꾸기만 했는데 쉬워졌다. 나는 이걸 한번에 떠올리지는 못해서 위의 삽질을 열심히 했다..
여튼 구하는 것을 바꾸기만 해도 쉽게 문제를 풀어나갈 수도 있는것이다.
여담으로, 코드에 Goldbach’s conjecture is wrong을 출력하게 해놓은 부분은 없다. 왜냐하면, 이 추측이 \(\small 10^{18}\)까지는 성립한다고 밝혀져 있어서 \(\small 10^{6}\)까지는 당연히 되야하니까..
코드 전문
6588 // 골드바흐의 추측
10 Aug 2021
난이도
Gold V
문제 풀이
간단하게 생각해보면, M개의 치킨집을 고르고 그 치킨집들에 대해 도시의 치킨거리를 구한다음, 도시의 치킨거리가 최소가 될때를 선택하면 해결된다. M개의 치킨집을 고르는 경우의 수는 최대 13개의 치킨집에서 M개를 고르는 것이므로 \(\small C(13, M)\)이다. 그 다음, 최대 2N개의 집에서 치킨 거리를 계산해야하니 \(\small O(2N) \cdot O(M) \cdot O(C(13, M)) = O(2NM \cdot C(13, M))\)이 된다. 최대값을 생각해보면 \(\small 10^{8}\)을 넘기지 않으니 1초 이내에 수행 가능하다. 따라서, 이 아이디어를 그대로 구현하면 답을 만들어낼 수 있다. 그대로 코드로 구현하면 아래와 같다.
void solve(int idx, vector<pair<int, int>>& chosenChicken, vector<pair<int, int>>& chicken, vector<pair<int, int>>& house, int& M) {
if(chosenChicken.size() == M) {
int chickenDist = 0;
for(auto& element : house) {
int hy = element.first;
int hx = element.second;
int minimum = abs(hx - chosenChicken[0].second) + abs(hy - chosenChicken[0].first);
for(auto& c : chosenChicken) {
int cy = c.first;
int cx = c.second;
minimum = min(minimum, abs(hx - cx) + abs(hy - cy));
}
chickenDist += minimum;
}
ret = min(ret, chickenDist);
return;
}
for(int i = idx; i < chicken.size(); ++i) {
chosenChicken.push_back(chicken[i]);
solve(i + 1, chosenChicken, chicken, house, M);
chosenChicken.pop_back();
}
}
먼저 함수에서 호출하는 파라미터들을 살펴보자
void solve(int idx, vector<pair<int, int>>& chosenChicken, vector<pair<int, int>>& chicken, vector<pair<int, int>>& house, int& M)
idx는 선택을 시작할 치킨집의 시작 인덱스를 말하는것이다. chosenChicken은 선택한 치킨집들이 모인 벡터이다. chicken, house, M은 각각 치킨집, 집, 선택할 치킨집의 수라는 정보를 담고 있도록 했다.
if(chosenChicken.size() == M)
이 조건은 기저조건으로, 고른 집들 개수가 M개이면 모두 선택한것이니 그 아래에서 치킨거리를 계산하도록 해놓았다.
for(int i = idx; i < chicken.size(); ++i) {
chosenChicken.push_back(chicken[i]);
solve(i + 1, chosenChicken, chicken, house, M);
chosenChicken.pop_back();
}
이 부분에서 치킨집을 고르게 된다. 먼저 idx부터 시작해 chosenChicken에 넣는다. 그 다음, i + 1번째 인덱스를 가르키게 하여 재귀함수를 호출하여 똑같은 과정을 하게 한다. 호출이 끝나면, chosenChicken에 담았던 치킨집을 제거한다. 그럼 for문이 i를 증가시키고 다음 치킨집을 넣고 재귀함수 호출하고 빼고 하는 과정을 계속 할 것이다. 이렇게 조합을 구현할 수 있는 것이다.
이렇게 치킨집조합을 구해 chosenChicken의 크기가 M이 되었으면 위의 if문에 걸려 들어가게 된다. 그럼 거기서 치킨거리를 계산해주면 끝이다. 거리를 계산하는 과정은 다음과 같다.
if(chosenChicken.size() == M) {
int chickenDist = 0;
for(auto& element : house) {
int hy = element.first;
int hx = element.second;
int minimum = abs(hx - chosenChicken[0].second) + abs(hy - chosenChicken[0].first);
for(auto& c : chosenChicken) {
int cy = c.first;
int cx = c.second;
minimum = min(minimum, abs(hx - cx) + abs(hy - cy));
}
chickenDist += minimum;
}
ret = min(ret, chickenDist);
return;
}
모든 집들에 대해 치킨거리를 구해 도시의 치킨거리에 더해준다. 그리고 전역변수로 선언된 ret에 최소값을 저장해주는 식이다. 그렇게 함수가 전부 호출이 끝나면, ret에는 답이 저장되어있으니 그걸 출력해주면 된다.
완전탐색으로 쉽게 해결할 수 있는 문제였다. 근데, 나는 이 문제 푸는데 곤혹을 겪었는데.. 그 이유는 solve(i + 1, …) 부분에 i대신 실수로 idx를 넣어서 시간복잡도가 매우 크게 되어버렸기 때문이다. 그래서 처음에는 TLE를 받았는데 저걸 찾고 제출하니 맞았다. 어이없는 실수이지만 찾기 어려운 실수라 조심할 필요가 있다. 저걸 idx로 넣게 되면 어떤일이 발생하게 되냐면, 쓸데없는 중복이 계속 발생하게 되어서 필요없는 연산을 무지성으로 반복하게 된다.
코드 전문
15686 // 치킨 배달
22 Jul 2021
난이도
Silver I
문제 풀이
N의 최대값이 1024이고 M의 최대값이 100000으로 주어져 있다. 시간제한이 1초이기에 좌표 2개가 주어질 때마다 구간에서 합을 구하려고 한다면, 당연하게도 시간초과가 난다. 따라서, 이 문제는 DP를 이용해 풀 필요가 있다. 먼저, 두 좌표가 주어졌을 때, 어떻게 하면 그 구간에서의 합을 구할 수 있을까?
단순히 생각해보면, 그냥 \(\small (x_1 \leq i \leq x_2, y_1 \leq j \leq y_2)\)을 만족하는 (i, j)에 대해 (i, j)에 있는 수를 모두 더하면 될 일이다. 그러나, 이런식으로 코드를 짜게 된다면 필연적으로 시간초과를 맞이하게 된다.
\(\small (x_2 - x_1) \times (y_2 - y_1) \leq O(N^2)\) 만큼의 연산이 주어진 좌표마다 수행되게 되니,
\(\small O(M) \times O(N^2) = O(MN^2)\)이 되므로, 주어진 시간 내에 수행이 불가하다. 그럼, 저렇게 더하는 시간을 줄일 필요가 있는데.. 이를 해결하기 위해서 나는 (1, 1)에서 (x, y)까지의 합을 따로 저장하는 방법을 떠올렸다.
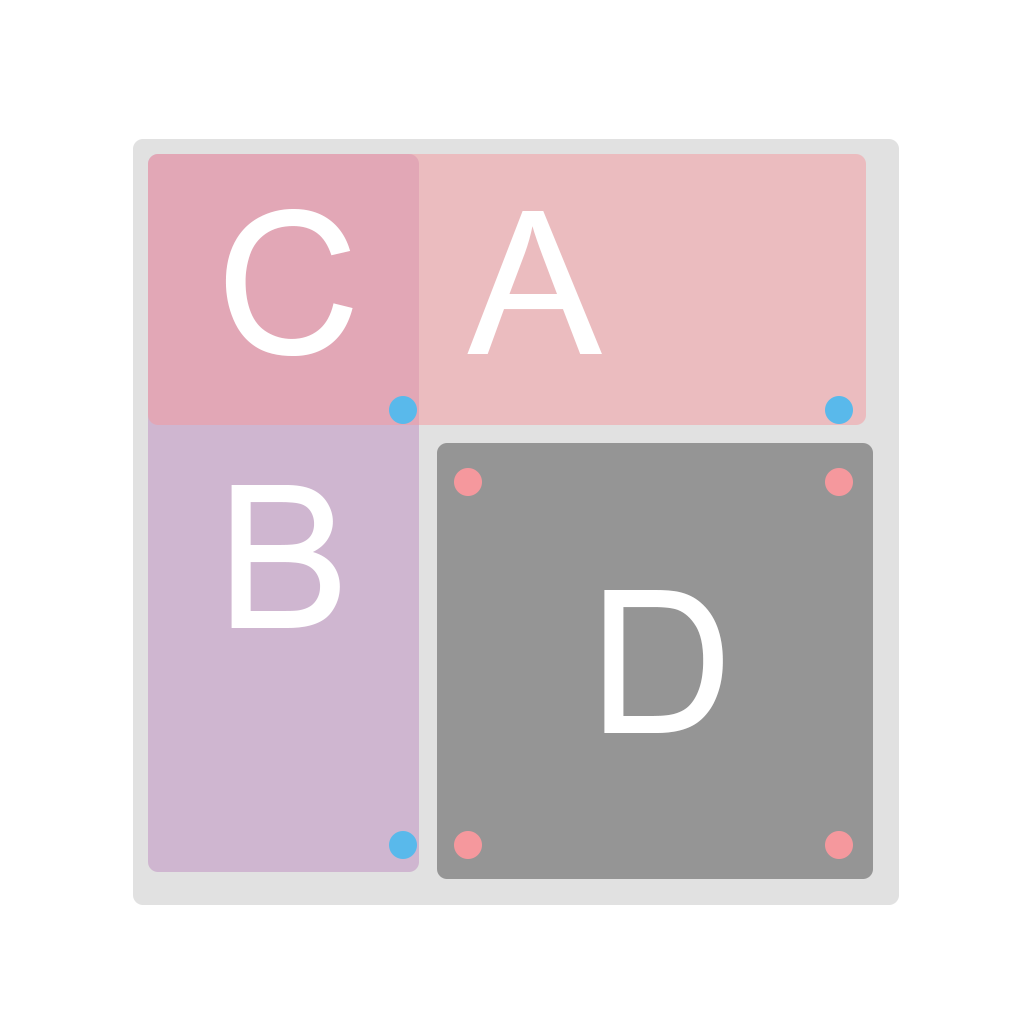
그렇게 따로 저장을 하면 우리가 구하고 싶은 영역인 D는 \(\small D = (all) - A - B + C\)로 구할 수 있게 된다. 문제에서 주어지는 점들을 빨간 점들로 표시해놨는데, 이 점들로부터 파란점들을 얻어내면 이런 방식으로 합을 구할 수 있게 된다. 이것을 수식으로 표현하면, \(\small S = sum(x_2, y_2) - sum(x_1 - 1, y_2) - sum(x_2, y_1 - 1) + sum(x_1 - 1, y_1 - 1)\)라고 쓸 수 있다. (이때, sum(x, y)는 (1,1)부터 (x, y)까지의 합)
그러면, sum에 해당하는 값들만 미리 구해놓으면 어떤 값이 들어오든 \(\small O(1)\)안에 해결할 수 있게 된다. \(\small dp[x][y]\)를 “(1, 1)에서 (x, y)까지의 합”으로 정의하자. 이 dp배열 값들을 미리 구하면 되는데, 이 값을 구할 때 무턱대고 반복문으로 합을 구해 저장하게 된다면, 위에서 \(\small O(MN^2)\)의 복잡도를 가지는 방법과 별반 다를게 없게 된다. 그렇기 때문에, 연산 횟수를 최대한 줄이기 위해 이전 합을 이용해서 다음 합을 구하면 좋을 듯 하다.
\[dp[1][2] = dp[1][1] + value[1][2]\]
\[dp[1][3] = dp[1][2] + value[1][3]\]
…
\[dp[3][2] = dp[3][1] + (value[1][2] + value[2][2] + value[3][2])\]
…
처럼 쓸 수 있음을 생각해보면, dp점화식은 다음처럼 쓸 수 있다.
\[dp[x][y] = dp[x][y - 1] + \sum_{k = 1}^{x}value[k][y]\]
요런 점화식으로 값을 구한다면, 뒤의 Sum에 의해 연산횟수가 결정된다는 것을 알 수 있다. 이렇게 구하면 확실히 이전 방법보다는 연산횟수가 많이 줄어든다는 것을 알 수 있다. 이 점화식을 가지고 코드를 아래처럼 짤 수 있다.
for(int i = 0; i <= N; ++i) {
dp[i][0] = 0;
dp[0][i] = 0;
}
for(int i = 1; i <= N; ++i) {
for(int j = 1; j <= N; ++j) {
int summation = 0;
for(int n = 1; n <= i; ++n) {
summation += map[n][j];
}
dp[i][j] = dp[i][j - 1] + summation;
}
}
각각 x = 0, y = 0 이 되는 부분은 0으로 처리를 해주었고, 위의 식을 그대로 옮겨 dp배열의 값을 저장하도록 했다. 이후 \(\small S = sum(x_2, y_2) - sum(x_1 - 1, y_2) - sum(x_2, y_1 - 1) + sum(x_1 - 1, y_1 - 1)\) 이 식을 이용해 좌표가 들어올 때마다 정답을 출력하도록 코드를 짜면 끝이다. 물론 저 summation부분도 또 다른 dp로 최적화 해줄 수 있겠지만, 굳이 그러지 않아도 1초안에 해결된다.
코드 전문
11660 // 구간 합 구하기 5
07 Jul 2021
난이도
Silver I
문제 풀이
문제에서 가장 까다로운 부분은 1과 2만큼 성장시키는 물뿌리개를 동시에 사용해야 한다는 점이다. 물뿌리개가 한 번 시행할 때 마다 어디에 뿌려지고, 어떤 물뿌리개를 쓰는지 생각하는 식으로 문제를 해결하려하면 매우 어려울 것이다. 따라서, 그런 순서를 무시하는 방법으로 문제를 접근하는 편이 옳다고 생각한다.
최종적으로 가능한 경우의 나무 배치라면, (1 성장 물뿌리개 사용 횟수) = (2 성장 물뿌리개 사용 횟수) 임을 자명하게 알 수 있다. 즉, 어떤 순서로 뿌려졌고 어떤 물뿌리개가 쓰였는지 몰라도, 사용횟수가 동일하게 나온다면 순서는 알아서 끼워맞춰진다고 생각할 수 있으니, 사용횟수가 같아질 수 있는지만 체크해주면 되는 것이다.
void solve(int* height, int N) {
int oneCnt = 0, twoCnt = 0;
for(int i = 0; i < N; ++i) {
if(height[i] % 2) oneCnt++;
twoCnt += (int)height[i] / 2;
} //save maximum quotient of two and minimum of one
while(true) {
if(twoCnt == oneCnt) { //'oneCnt == twoCnt' means you can grow trees.
cout << "YES";
break;
}
twoCnt -= 1; //if not, increase oneCnt (2 = 1 * 2)
oneCnt += 2;
if(twoCnt < oneCnt) { //if oneCnt is more than twoCnt, it means you can't grow trees.
cout << "NO";
break;
}
}
}
height는 배열로, 입력받은 나무 배치들의 정보가 담겨있고, N은 심은 나무의 개수이다.
int oneCnt = 0, twoCnt = 0;
for(int i = 0; i < N; ++i) {
if(height[i] % 2) oneCnt++;
twoCnt += (int)height[i] / 2;
} //save maximum quotient of two and minimum of one
이 블럭에서, oneCnt, twoCnt라는 변수에 각각의 사용횟수를 기록한다. (twoCnt가 최대가 되는 방향으로 설정함.)
while(true) {
if(twoCnt == oneCnt) { //'oneCnt == twoCnt' means you can grow trees.
cout << "YES";
break;
}
twoCnt -= 1; //if not, increase oneCnt (2 = 1 * 2)
oneCnt += 2;
if(twoCnt < oneCnt) { //if oneCnt is more than twoCnt, it means you can't grow trees.
cout << "NO";
break;
}
}
while문에서 twoCnt = oneCnt인지 지속적으로 체크한다.
만약 두 물뿌리개의 사용횟수가 같아질 수 있다면, 가능하므로 YES를 출력하고 종료한다.
같지 않다면, (2 성장 물뿌리개)의 사용횟수를 하나 줄이고 (1 성장 물뿌리개)의 사용횟수를 두개 늘려가며 반복문을 돈다.
만약, twoCnt < oneCnt가 되어버리면 불가능한 경우이기에 NO를 출력하고 종료한다.
(twoCnt를 최대로 설정했기에 줄어들며 oneCnt보다 작아진다면, 당연히 같아질 수 없다.)
이렇게 횟수가 같아질 수 있는지만 체크해 출력해주면 되는 문제인 것이다.
발상의 방향이 중요한 비교적 간단한 문제.
코드 전문
19539 // 사과나무(UCPC 2020 Qualifier H)
