[머신러닝] Linear Regression 선형 회귀 분석
20 Sep 2021Linear Regression
고등학교 다닐때 잠시 배워보고 접었던 머신러닝을 다시 배워보려고 하고 있다. coursera.org에서 Andrew Ng 교수님의 Machine Learning 강의로 배워보는 중이다. 그때나 지금이나 이해하는 능력자체는 슬프게도 비슷한 것 같다. 여튼 2주차까지 들어보고 하니 이제 대충 Linear Regression에 대해 이해가 되는 듯 싶다.
Linear Regression, 한국어로 하자면 “선형 회귀“라는 의미이다. 말이 뭔가 어려운데, 간단하게 말해보자면 주어진 데이터셋을 가장 잘 표현할 수 있는 선형적인 함수를 찾는 문제이다.
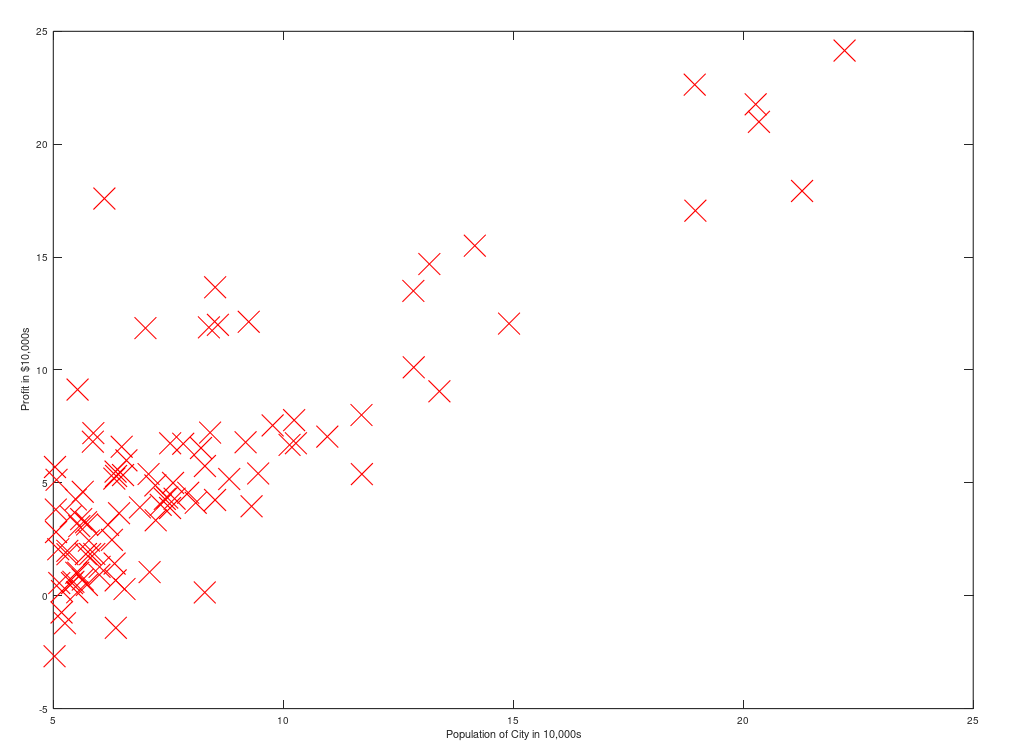
이런 데이터셋이 주어졌을때, 아래의 그림처럼 파란색의 선형적인 함수를 찾는게 바로 선형회귀인것이다.
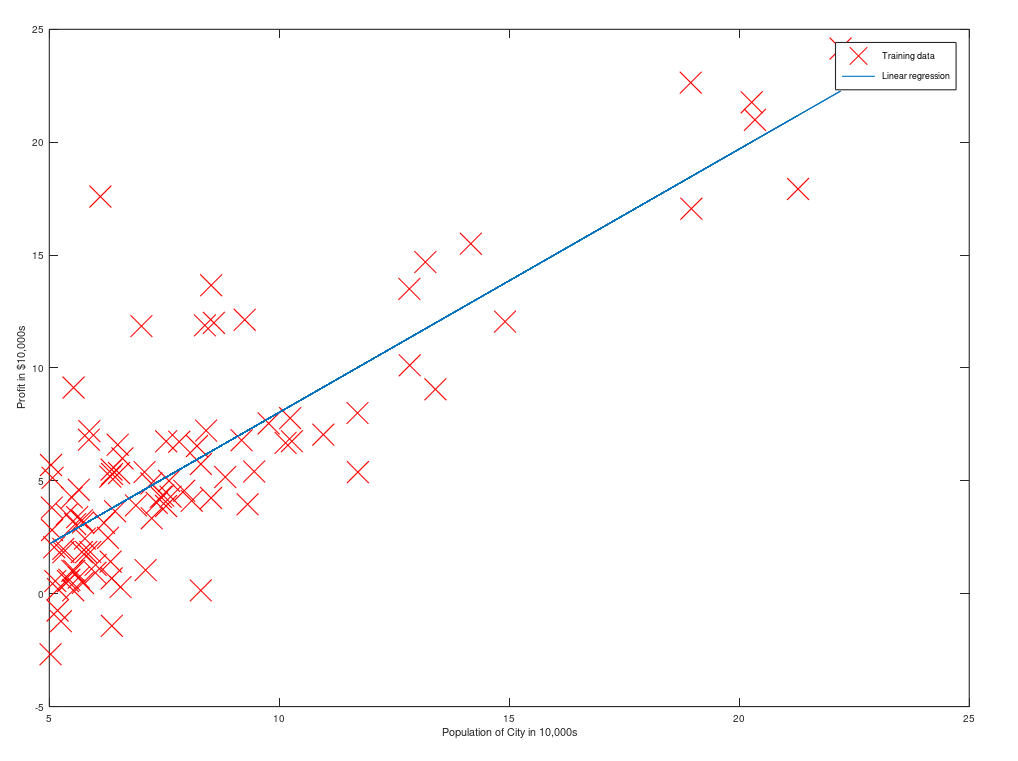
(데이터셋 출처 : Machine Learning - Andrew Ng 강의에서 2주차 과제)
(x는 각각의 데이터 값이고, y는 그 입력데이터 값에 대한 답, h(x)에서 도출 되는 값은 가설함수가 예측하는 모델의 값).
그럼, 이걸 어떻게 하느냐? 데이터를 표현하는 함수를 가설함수 h(x)라고 해보자. 그러면, \(\scriptsize abs(h(x) - y)\)의 합이 최소가 되는 함수 h가 곧 답이 되지 않을까? 즉, 예측값과 실제값과의 차이가 가장 적은 가설함수 모델이 가장 적합할 것이라는 소리이다. 대충 어떻게 해야 되는지 알았으니 한번 해보도록 하자. 먼저, »Linear« Regression이라는 이름에 맞게 가설함수를 \(\small h_{\theta}(x) = \theta^{T}x\)라고 하자. 이때, 세타와 x값은 열벡터로 주어진다. 세타의 transpose에 x를 곱하면 \(\scriptsize \theta_{0}x_{0} + \theta_{1}x_{1} + ...\) 같은 선형함수꼴로 나타남을 알 수 있다. x의 차원은 feature 개수를 몇개로 하느냐에 따라 달라진다. 여튼 이렇게 표현되는 가설함수를 이용해서 함수 하나를 새로 만들어보자
\[J(\theta) = \frac{1} {2m}\sum_{i=1}^{m}(h_{\theta}(x^{(i)}) - y^{(i)}) ^ {2}\]
함수 J(비용함수)를 이런식으로 한번 정의해보자. 이때, m은 데이터의 개수이다. 즉, 식의 의미는 데이터 분산의 1/2 이다. 이 J라는 함수는 가설함수가 예측한 값과 실제값이 얼마나 떨어져 있는지 잘 나타내주니(분산이 그런 의미니까) 떨어져 있는 정도가 최소가 되는 세타값들을 찾아주면 된다. 최소값을 어떻게 구하냐..? 대충 2가지 정도가 있다.
1. Gradient Descent
2. Normal Equation
Gradient Descent는 J를 편미분해 찾은 값으로 그래프의 경사를 따라 내려오며 local minimum을 찾는 알고리즘이고, Normal Equation은 그냥 \(\scriptsize J'(\theta) = 0\)이 되는 세타값을 수식으로 찾아주는 방법이다.(미분계수가 0인 지점에서 극소값을 가지기 때문임.)
후자의 Time Complexity는 \(\scriptsize O(N ^ {3})\)인 반면, Gradient Descent는 잘만 만들어주면 그것보단 빠르게 값을 찾을 수 있다. 즉, 데이터 크기가 작을때는 그냥 Normal Equation으로 값을 구하되, 크기가 커지면 Gradient Descent를 이용해서 찾아주면 되는 것이다.
먼저 Gradient Descent를 간단하게 알아보자. 그래프에서 가파른 부분을 따라 내려가주면 local minimum을 찾을 수 있다는 것은 자명하다. 그렇기 때문에 \(\scriptsize \theta := \theta - \alpha \cdot J'(theta)\)를 해주면 되지 않을까? \(\small \alpha\)의 값은 빠르게 수렴할 수 있는 크기로 설정해주면 된다. 아래는 위 식을 풀어서 정리한 식이다. 알파와 m을 제외한 모든값은 벡터라고 생각하면 된다.
\[\theta := \theta - X^{T}(X \theta - y) \cdot (\frac{\alpha}{m})\]
이 과정을 여러번 해주면 결국엔 Local Minimum으로 수렴하게 되고, 우리가 원하는 세타값을 찾을 수 있게 된다. 근데, 이 알고리즘 말은 쉽지만, 사실 해줘야할게 좀 많다. Learning Rate라고 불리는 \(\small \alpha\)값도 설정해주어야하고, 수렴하는지 여부도 체크해줘야한다. 또한, 각각의 feature가 극단적인 scale을 가진다면(x1이 (-1, 1)인데 x2가 (-10000000, 10000000) 이런식인 경우) feature scaling을 통해 범위를 맞춰야만 하는 번거로움이 있다. 그래서 데이터 수가 적을때는 Normal Equation을 사용하는 쪽이 더 간편하다.
Normal Equation은 식을 이러쿵 저러쿵 조작해서 J’이 0이 되는 theta를 직빵으로 얻어낼 수 있는 방법이다. 아래의 식으로 해결할 수 있다.
\[\theta = (X^{T}X) ^ {-1} X^{T}y\]
이게 Inverse를 계산하는데 \(\scriptsize O(N ^ {3})\) cost가 소요되어서 느리긴 하지만, 저 식만 써주면 그냥 바로 찾아낼 수 있는 간편함을 보여준다.
이런 두 방법으로 J가 최소가 되는 세타를 찾을 수 있다. 그런데.. 선형함수말고는 못하는걸까? 사실 그런것도 아니다.. 당연히 가능하다. 단지 비선형으로 나타내어진 h를 선형으로 고치기만 하면 위 내용을 그대로 적용할 수 있기에, 문제될 것도 없다. 즉, \(\scriptsize h(x) = \theta_{0} + \theta_{1}x_{1} + \theta_{2}x_{2}^{2}\) 처럼 주어지면, 새로운 변수 \(\scriptsize x'_{2} = x_{2}^{2}\)라고 하면 그만이다. 그냥 비선형적인 요소들을 모조리 바꿔주면 Linear Regression을 적용시킬 수 있다.
여튼 최근에 이런 내용들을 배워보고 있다. 아직까진 재밌는 것 같은데.. 점점 수식이 뜬금없이 툭툭하고 튀어나오니 슬슬 어지러워지기 시작하고 있다. 수학을 그닥 잘하는 편이 아닌지라,, 올해 안에 과연 제대로 다 배울 수 있을까?