DSU로 미로 만들기

Disjoint-Set & Union-Find

자료구조론 시간에 재밌는 과제가 나와서 한 번 정리해보려고 한다. 보통 유니온-파인드라고 많이 부르는 알고리즘으로 미로를 만들 수가 있다.

일단 Disjoint-Set이 무엇인지부터 알아보자.

Disjoint-Set은 교집합이 없는 2개 이상의 분리되어 있는 집합(쉽게 말해서 서로소 집합)이라고 할 수 있다. 이 집합에서는 합집합 연산(Union)을 할 수 있다. 집합은 inverted(child가 parent를 가르킨다는 의미) tree 형태로 표현할 수 있다. 각 트리의 루트는 하나로 유일하기 때문에, 루트를 비교하는 것으로 같은 집합인지 확인 할 수 있다.

Find

parent[x]를 x의 부모 노드라고 정의하면, 다음과 같이 find 연산을 구현할 수 있다. 이때, 부모 노드가 없는 경우엔 parent[x] = x 가 된다.

int find(int x) {
    if(x == parent[x]) return x;
    else return parent[x] = find(parent[x]); //path compression
}

각 parent노드를 최상위 루트 노드에 달아버리는 path compression을 사용하면 find 연산 시간이 상당히 빨라진다.

Union

합집합 연산은, 각 집합의 루트를 찾아낸 다음 루트를 합치는 식으로 구현할 수 있다.

void uni(int x, int y) {
    int x_p = find(x);
    int y_p = find(y);

    if(x_p == y_p) return;
    
    if(x_p < y_p) parent[y_p] = x_p;
    else parent[x_p] = y_p;
}

Union을 할때, rank를 사용해 rank가 큰 쪽에 낮은걸 합쳐주게 되면 시간복잡도가 향상된다. path-compression과 union-by-rank를 모두 사용해 최적화 해주게 되면, \(\scriptsize O(\alpha(N))\)이다. path-compression만 사용해도 상당히 빠르기 때문에, 나는 보통 path-compression만 사용한다.

N x N 미로 만들기

이런 자료구조랑 알고리즘을 사용해서 N x N크기의 미로를 생성하는 프로그램을 짤 수 있다. (와!)

모든 칸의 테두리에 벽이 있다고 가정하면, 아래와 같은 과정을 통해서 미로를 생성해낼 수 있다.

while(find(첫칸) != find(마지막칸)) {
    x = 랜덤으로 선택한 벽
    a = x에 붙어있는 첫번째 칸
    b = x에 붙어있는 두번째 칸

    if(find(a) != find(b)) {
        x를 지운다.
        uni(a, b)
    }
}

즉, 첫칸과 마지막칸이 같은 집합이 될 때까지 벽을 없애면서 공간을 합쳐주는 식으로 미로를 만들 수 있다. 근데 막상 구현하려고 하니, 벽을 없애는 부분이 조금 까다로웠다. 나는 모든 벽을 모두 저장하지 않고 필요한 벽만 저장하는 방식으로 구현을 했다. 잘 생각해보면, 한 칸당 _| 벽만 있어도 모든 걸 다 구현할 수 있다는 사실을 깨달을 수 있다. 그렇기에 총 \(\scriptsize 2n^{2}\)개의 벽이 필요하고, 아래 그림처럼 번호를 생각해주면, 각 벽을 허물었을 때 어느 칸이 합집합이 되는 지 쉽게 알 수 있다. 요걸 가지고 잘 구현만 해주면 미로를 생성할 수 있다.

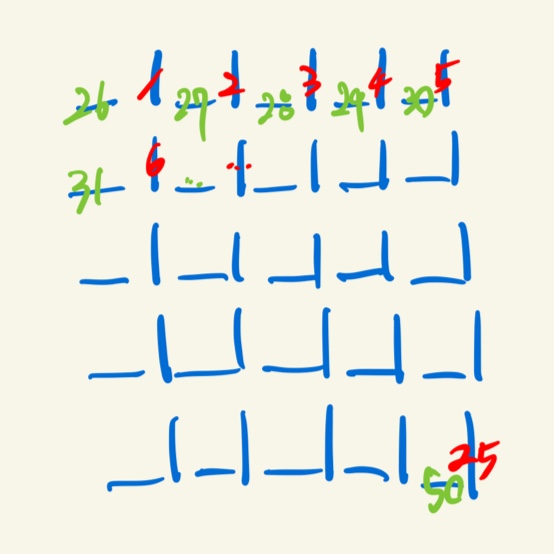
edit : 2022-08-18 01:07 1학기 끝난 지 한참 지났기 때문에 그때 짰던 과제 코드도 첨부합니다.

void createMaze(DisjointSets* sets, PrintDisjointSets* maze, int n) {
    srand(time(NULL));
    int s = n * n;
    while(find(sets, 1) != find(sets, s)) {
        int wall = rand() % (2 * s) + 1;

        //horizontal merge
        if(1 <= wall && wall <= s) {
            int cell_a = wall;
            int cell_b = cell_a + 1;
            if(cell_a % n == 0) continue;
            if(find(sets, cell_a) != find(sets, cell_b)) {
                maze->ptr_arr[wall] = 0;
                union_(sets, cell_a, cell_b);
            }
        }
        //vertical merge
        else {
            int cell_a = wall % s;
            if(cell_a == 0) cell_a = s;
            int cell_b = cell_a + n;

            if(cell_b > s) continue;

            if(find(sets, cell_a) != find(sets, cell_b)) {
                maze->ptr_arr[wall] = 0;
                union_(sets, cell_a, cell_b);
            }
        }
    }   
}

void printMaze(PrintDisjointSets* maze, int n) {
    int s = n * n;
    maze->ptr_arr[s] = 0;
    for(int i = 0; i < n; ++i) printf(" -");
    printf("\n");

    for(int i = 0; i < n; ++i) {
        if(i != 0) printf("|");
        else printf(" ");

        for(int j = 1; j <= n; ++j) {
            char x = (maze->ptr_arr[i * n + j] ? '|' : ' ');
            printf(" %c", x);
        }
        printf("\n");

        for(int j = 1; j <= n; ++j) {
            char x = (maze->ptr_arr[i * n + j + s] ? '-' : ' ');
            printf(" %c", x);
        }
        printf("\n");
    }
}

createMaze함수는 말 그대로 위의 방식으로 벽을 골라 지워 미로를 만드는 함수다. printMaze함수는 만들어진 미로를 출력하는 함수다.

좌우 셀을 합칠 땐, 현재 셀 번호가 \(\scriptsize k\)일때, \(\scriptsize (k, k + 1)\)셀을 합치면 된다. 상하 셀을 합칠 땐, \(\scriptsize (k, k + n)\)셀을 합치면 된다. 셀 번호를 찾으려면 위에서 소개한 방법으로 벽을 넘버링 하면 편하기 때문에 그렇게 설계했었다.

아마 코드를 보면 쉽게 이해가 될 것 같다. 자료구조론 같이 강의 듣던 친구가 어떻게 만들었냐고 묻길래 내 방법 설명해주니까 그냥 뚝딱뚝딱 만들어 오는걸 보면.. 이 방법이 그렇게 어렵진 않은 듯?