Google Code Jam 2022 Qualification Round (구글 코드잼 예선)
03 Apr 2022Google Code Jam Qualification Round
퀄리피케이션 라운드는 30점만 긁으면 다음 라운드로 나갈 자격이 주어진다. 이번 라운드에서는 A, B, C를 차례로 풀기만 해도 44점이라 3문제만 풀면 됐었다. 나는 A, B, C, D를 풀고 E는 상당히 어려워보이는 문제라 풀진 않고 넘어갔다.
나는 71점 전체 749등으로 마무리했다.

A. Punched Cards
지문에 쓸데 없는 내용이 가득한데, 그냥 단순한 구현 문제이다. 좌측 상단 4칸만 ‘.’으로 채워주고 나머지는 규칙에 따라 채운 뒤 출력해주면 된다.
코드 보기
#include <bits/stdc++.h>
using namespace std;
int main() {
ios_base::sync_with_stdio(false);
cin.tie(nullptr);
cout.tie(nullptr);
int T; cin >> T;
int tc = 1;
while(T --> 0) {
int R, C; cin >> R >> C;
vector<vector<char>> m(2 * R + 1, vector<char>(2 * C + 1));
for(int i = 0; i < R; ++i) {
for(int j = 0; j < C; ++j) {
int r = 2 * i, c = 2 * j;
m[r][c] = '+';
m[r + 1][c] = '|';
m[r][c + 1] = '-';
m[r + 1][c + 1] = '.';
}
}
m[0][0] = m[1][0] = m[0][1] = m[1][1] = '.';
for(int i = 0; i < C; ++i) {
m[2 * R][2 * i] = '+';
m[2 * R][2 * i + 1] = '-';
}
for(int i = 0; i < R; ++i) {
m[2 * i][2 * C] = '+';
m[2 * i + 1][2 * C] = '|';
}
m[2 * R][2 * C] = '+';
cout << "Case #" << tc++ << ":\n";
for(int i = 0; i <= 2 * R; ++i) {
for(int j = 0; j <= 2 * C; ++j) {
cout << m[i][j];
}
cout << '\n';
}
}
return 0;
}
B. 3D Printing
Cyan 색상을 세 프린터에서 쓸 수 있는 최대한으로 쓰고 싶다고 해보자. 주어지는 Cyan 용량 값들 중 최솟값이 Cyan을 최대한으로 쓸 수 있는 값이다(예를 들어, 10, 5, 3이 주어지면 3보다 더 쓸 수 없으니..). 따라서, 이와 같이 모든 컬러에 대해 최솟값을 찾아주고 “min(C) + min(M) + min(Y) + min(K) >= 1e6”이면, 가능한 케이스 이므로 실제 답을 찾아서 출력해주고, 그렇지 않으면 불가능한 케이스이니 IMPOSSIBLE을 출력하면 된다.
코드 보기
#include <bits/stdc++.h>
using namespace std;
using ll = long long;
using pii = pair<int, int>;
using ppii = pair<int, pii>;
int main() {
ios_base::sync_with_stdio(false);
cin.tie(nullptr);
cout.tie(nullptr);
int T; cin >> T;
for(int tc = 1; tc <= T; ++tc) {
int C[3], M[3], Y[3], K[3];
for(int i = 0; i < 3; ++i) cin >> C[i] >> M[i] >> Y[i] >> K[i];
bool flag = false;
int min_C = *min_element(C, C + 3);
int min_M = *min_element(M, M + 3);
int min_Y = *min_element(Y, Y + 3);
int min_K = *min_element(K, K + 3);
if(min_C + min_M + min_Y + min_K >= int(1e6)) flag = true;
cout << "Case #" << tc << ": ";
if(!flag) cout << "IMPOSSIBLE";
else {
int s = 1e6;
int min_color[4] = {min_C, min_M, min_Y, min_K};
for(int i = 0; i < 4; ++i) {
if(s - min_color[i] < 0) {
min_color[i] = s;
s = 0;
}
else s -= min_color[i];
}
for(int i = 0; i < 4; ++i) cout << min_color[i] << ' ';
}
cout << '\n';
}
return 0;
}
C. d1000000
1부터 차례대로 증가하게 주사위를 배치할 때, 얼마까지 수가 증가할 수 있는지 묻는 문제이다. Greedy하게 생각해보면, 먼저 Si가 작은 값부터 차례대로 정렬시켜 놓자. 배치하는 수는 1부터 시작하고, 그 숫자를 x라고 해보자. 정렬되어 있는 수열에서 앞에서부터 차례로 비교하자. x <= Si이면 가능하기 때문에, x와 인덱스를 함께 증가시켜주면 되고, x > Si이면 x <= Sk를 만족하는 최초의 인덱스 k를 찾으면 된다(못찾으면 그대로 끝). 이렇게 x를 찾아주면, 마지막에는 답이 되는 수보다 1만큼 크기 때문에, -1해서 출력해주면 정답.
코드 보기
#include <bits/stdc++.h>
using namespace std;
using ll = long long;
using pii = pair<int, int>;
using ppii = pair<int, pii>;
int main() {
ios_base::sync_with_stdio(false);
cin.tie(nullptr);
cout.tie(nullptr);
int T; cin >> T;
for(int tc = 1; tc <= T; ++tc) {
int N; cin >> N;
vector<int> d(N);
for(int& e : d) cin >> e;
sort(d.begin(), d.end());
int max_n = 1;
for(int i = 0; i < N; ++i, ++max_n) {
if(max_n > d[i]) {
while(i < N && d[i] < max_n) ++i;
if(i == N) break;
}
}
cout << "Case #" << tc << ": ";
cout << max_n - 1 << '\n';
}
return 0;
}
D. Chain Reactions
재밌는 문제였다. 신기했던 포인트가 있는데 문제에서 주어지는 그래프가 DAG임을 좀 특이한 형태로 알려주고 있다. 한 노드 a가 포인팅하는 다른 노드 b는 a > b를 만족해야한다는 성질이 그래프를 DAG로 고정시켜버린다. DAG임을 알고 나면, DAG DP를 시도해볼 수 있다. 나는 Topology Sort + DP로 문제를 해결했다.
풀이는 다음과 같다. (사진으로 대체함)
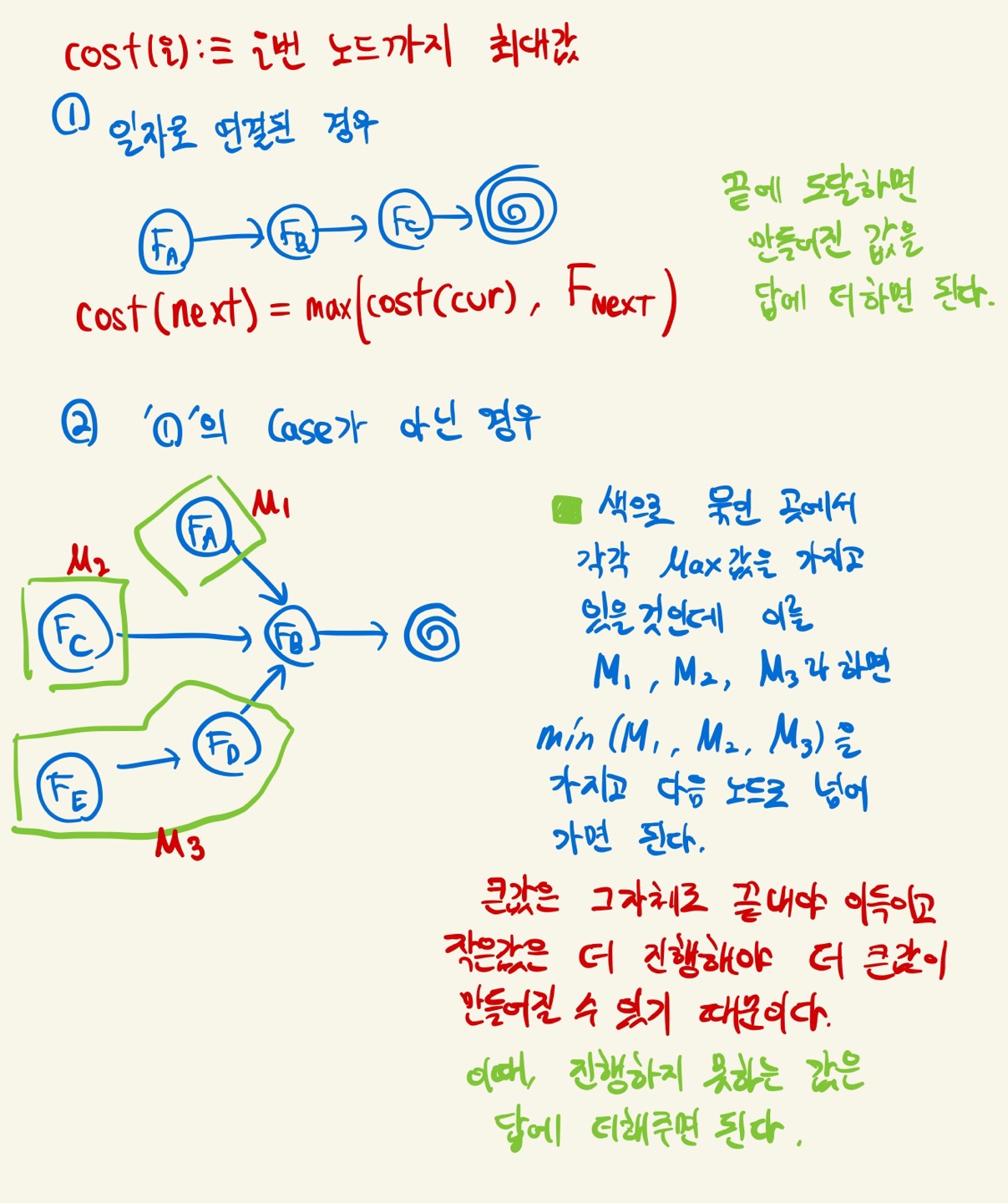
코드 보기
#include <bits/stdc++.h>
using namespace std;
using ll = long long;
using pii = pair<int, int>;
using ppii = pair<int, pii>;
const ll INF = 1'000'000'000'000'000'000LL;
ll solve(vector<vector<int>>& adj, vector<ll>& F, vector<int>& in_degree, int& N) {
vector<ll> cost(N + 1, INF);
queue<int> q;
for(int i = 1; i <= N; ++i) {
if(in_degree[i] == 0) {
cost[i] = F[i];
q.push(i);
}
}
ll ret = 0;
while(!q.empty()) {
int cur_node = q.front();
q.pop();
for(int& next_node : adj[cur_node]) {
if(next_node == 0) ret += cost[cur_node];
else if(cost[next_node] == INF && in_degree[next_node] == 1) {
cost[next_node] = max(cost[cur_node], F[next_node]);
in_degree[next_node]--;
q.push(next_node);
}
else {
cost[next_node] = min(cost[next_node], cost[cur_node]);
ret += cost[cur_node];
if(--in_degree[next_node] == 0) {
ret -= cost[next_node];
cost[next_node] = max(cost[next_node], F[next_node]);
q.push(next_node);
}
}
}
}
return ret;
}
int main() {
ios_base::sync_with_stdio(false);
cin.tie(nullptr);
cout.tie(nullptr);
int T; cin >> T;
for(int tc = 1; tc <= T; ++tc) {
int N; cin >> N;
vector<ll> F(N + 1);
for(int i = 1; i <= N; ++i) cin >> F[i];
vector<int> in_degree(N + 1);
vector<vector<int>> adj(N + 1);
for(int i = 1; i <= N; ++i) {
int Pi; cin >> Pi;
adj[i].push_back(Pi);
in_degree[Pi]++;
}
cout << "Case #" << tc << ": ";
cout << solve(adj, F, in_degree, N) << '\n';
}
return 0;
}
E. Twisty Little Passages
Tourist도 5트하고 도망가길래 사실 풀 생각도 없었던 문제고.. 거기에 interactive 라는 문제 유형 덕에 진짜 그냥 읽기만 했다. 대충 랜덤으로 노드를 방문해서 통로 수를 기억해 두고 그 값의 평균 * 노드 수 해서 출력한다는 흐름의 풀이라는데… 어 음.. 짱짱 어려운 문제인것만 알 것 같다.
대략 일주일 뒤 Round 1A에서도 스무스하게 풀 수 있었으면 좋겠다. 여튼 나의 첫 구글 코드잼 퀄리피케이션 라운드였다.