[백준 BOJ] 4206. 피보나치 단어

05 Aug 2022

난이도

Diamond V

문제 풀이

피보나치 수열을 한 번 구해본 사람이라면 다들 알지만, \(\scriptsize F_{100}\)만 되어도 매우 크다. 따라서, Naive하게 스트링을 만들고 패턴 매칭하는 것으로는 풀 수 없다.

그럼, 뭔가 규칙성이 있고 이전 정보를 쓸 수 있겠지? 라는 생각으로 dp를 떠올려보자.

\(\small dp(i) := "i\)번째 피보나치 단어 수열과 \(\small p\)의 매칭 개수”

라고 정의하자. 그럼 대략 이런 관계식이 구해진다.

\(\small dp(i) = dp(i - 1) + dp(i - 2) + "i - 1\)번째와 \(\small i - 2\)번째를 이으면서 생기는 추가적인 매칭 개수”

당연한 소리다. (약간 분할정복같은 너낌..) 그럼 이제, 저 두 스트링을 이으면서 발생하는 추가적인 매칭을 구하는게 이 문제의 핵심이 된다. 직접 스트링을 만들고 잇는건 무리가 있으니 조금만 더 관찰을 해보자.

\[\small F(N) = \textbf{ F(N - 1) + F(N - 2) }\] \[\small F(N + 1) = F(N) + F(N - 1) = (F(N - 1) + \textbf{ F(N - 2)) + F(N - 1) }\] \[\small F(N + 2) = F(N + 1) + F(N) = ... = ... + \textbf{ F(N - 1) + F(N - 2) } + ...\] \[\small F(N + 3) = ... + \textbf{ F(N - 2) + F(N - 1) } + ...\]

즉, 다른 두 스트링을 합칠 때, 합쳐지는 그 부분이 반복이 된다. 처음엔 \(\scriptsize F(N - 1)\)과 \(\scriptsize F(N - 2)\)이 합쳐지고, 그 다음 스트링에서는 \(\scriptsize F(N - 2)\)와 \(\scriptsize F(N - 1)\)이 합쳐진다. 이게 쭉 반복되기 때문에, 우리는 \(\scriptsize F(N - 1), F(N - 2)\)을 합칠 때 발생하는 추가적인 매칭과 \(\scriptsize F(N - 2), F(N - 1)\)을 합칠 때 발생하는 추가적인 매칭을 구하면 문제를 풀 수 있다.

왼쪽 스트링의 오른쪽 끝에서부터 \(\scriptsize \mid p\mid - 1\)개를 가져오고 오른쪽 스트링의 왼쪽 끝에서부터 \(\scriptsize \mid p\mid - 1\)개를 가져와서 합치면, 합쳐져서 발생하는 모든 스트링을 검사할 수 있게 된다.

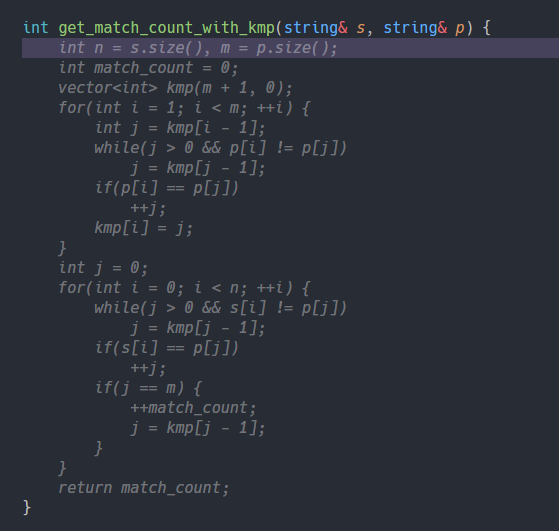
개수를 구하는 방법은 해싱이든 KMP든 \(\scriptsize O(N + M)\)에 매칭을 할 수 있는 알고리즘으로 하면 된다. 나는 KMP로 했다.

\(\scriptsize p\)의 길이보다 커지는 최초의 \(\scriptsize N\)을 찾아서 저걸 해주면 되는데, \(\scriptsize p\)가 100,000이니까 대충 30정도를 가져오면 된다. 30이전까지는 Naive하게 KMP를 돌려서 dp 배열을 채워주고, 30부터는 위의 방법을 적용시켜서 dp 배열을 채워나가면 된다.

concat_match[0] = get_match_count_with_kmp(s1, p);
concat_match[1] = get_match_count_with_kmp(s2, p);

for(int i = k, x = 0; i <= n; ++i, x = 1 - x) 
    dp[i] = dp[i - 1] + dp[i - 2] + concat_match[x];