[백준 BOJ] 10793. Tile Cutting
10 Jul 2022난이도
Diamond V
문제 풀이
요약하자면, 넓이가 \(\scriptsize S\)인 서로 다른 평행사변형들의 개수를 찾는 문제다. 문제를 처음보고 떠올린 풀이는 벡터를 여러개 만들어서 서로 외적시킨 다음, 외적의 크기로 어찌저찌 값을 구할 수 있지 않을까.. 였다. 뇌절 그 자체였다. \(\scriptsize O(NlogN)\) 개 정도의 벡터가 필요하지 않을까.. 생각하다가 조화급수부터해서 뇌절이 거듭되길래 도저히 말이 안되는 풀이같아서 그냥 자러갔다. (오후 1시에 자는 낮밤이 뒤바뀐 삶.. ㅋㅋ;;)
여튼, 자고 일어나서 다시 생각해서 도형을 직접 그려서 구하는걸 그려봤다.
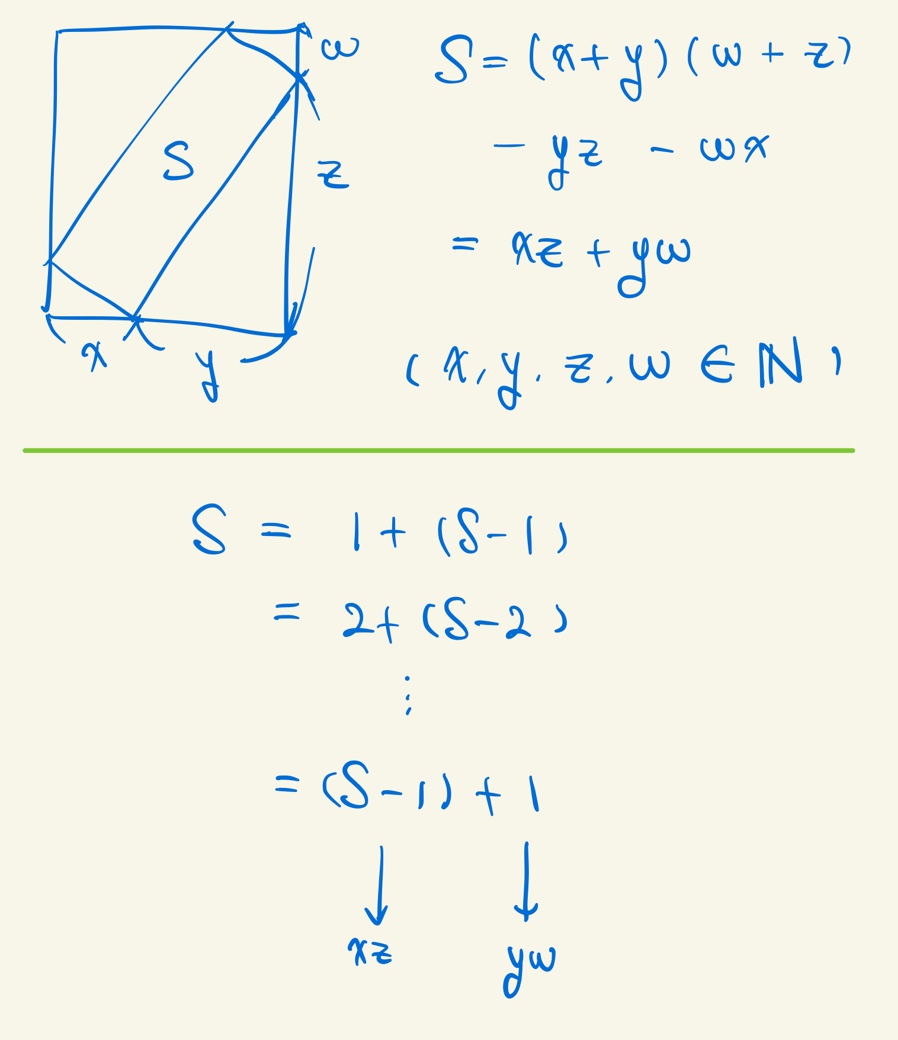
그림처럼 자연수 곱의 합으로 S를 표현할 수 있다. 두 자연수를 곱해서 \(\scriptsize k\)가 되는 경우의 수를 \(\scriptsize A_{k}\)라고 해보자. \(\scriptsize k = 1\)부터 \(\scriptsize k = S - 1\)까지 \(\scriptsize A_{k}A_{S-k}\)를 다 더해주면 그 값이 \(\scriptsize S\)일 때 평행사변형의 개수가 된다.

문제를 풀기 위해서는 \(\scriptsize S = 1\)부터 \(\scriptsize S = 500000\)까지 값이 필요하다. 따라서, \(\scriptsize A\)를 해당 범위까지 잘 구한 다음 convolution 해주면, 원하는 값을 얻을 수 있다.
\(\scriptsize n = 500\)이고, 쿼리 구간이 최대 \(\scriptsize 500000\)이라 쿼리 하나 처리하는데 \(\scriptsize O(N)\)이어서 TLE 날 것 같지만.. 의외로(?) 안난다. 세그먼트 트리 짜기가 귀찮아서 15초의 믿음을 가지고 제출했는데, 별 다른 최적화 없이도 500ms 부근으로 AC를 받을 수 있다. 총 시간 복잡도는 \(\scriptsize O(QN + NlogN)\)이다 (Q는 쿼리 개수, N은 500,000).