[백준 BOJ] 13055. K-inversions
05 Jul 2022난이도
Diamond V
문제 풀이
요약하자면, 단순히 inversion을 찾는 문제다. 그런데, 임의의 길이 K에 대해 K만큼 간격을 두고 떨어져있는 inversion 쌍들의 개수를 모두 세어 모두 출력해줘야하는 문제다. 요구하는건 분명 쉬운데.. 모든 길이의 inversion 쌍들을 다 찾아야 하는 점에서 문제가 어려워진다.
문제를 풀기 위해 주어진 걸 어떻게든 수식으로 바꿔보려 시도해보자. 먼저, B가 먼저 나오고 A가 나중에 나와야 inversion인 것은 자명하다. 다소 뜬금없지만, 이 성질을 이용해 아래 그림처럼 생각해 볼 수 있다.
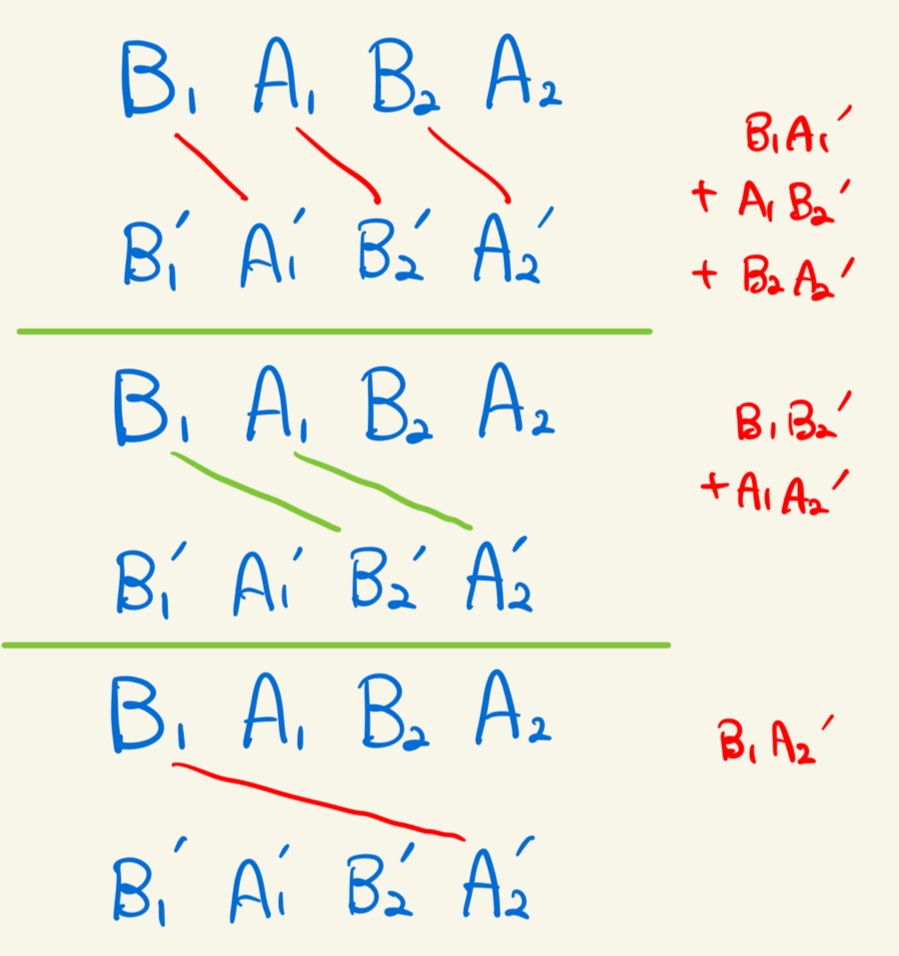
주어지는 스트링을 위 아래로 각각 두고, 위쪽은 \(\scriptsize B = 1, A = 0\)이라 하고 아래쪽은 \(\scriptsize B' = 0, A' = 1\)이라고 하자. 그럼 각 길이의 inversion 개수를 그림에 적힌 수식으로 전개할 수 있다. 그럼 저 값들을 찾아내는 것으로 문제가 변하는 데 Naive하게 생각하면 \(\scriptsize O(N^{2})\)임이 자명하고, 그렇게 풀면 TLE을 받는다.
따라서, \(\scriptsize O(N^{2})\)보다 빠른 풀이를 가져와야 한다.
식의 형태를 잘 관찰하고 있으면, convolution 꼴로 왠지 고칠 수 있을 것 같다(라는 느낌이 들어야하는 듯..).
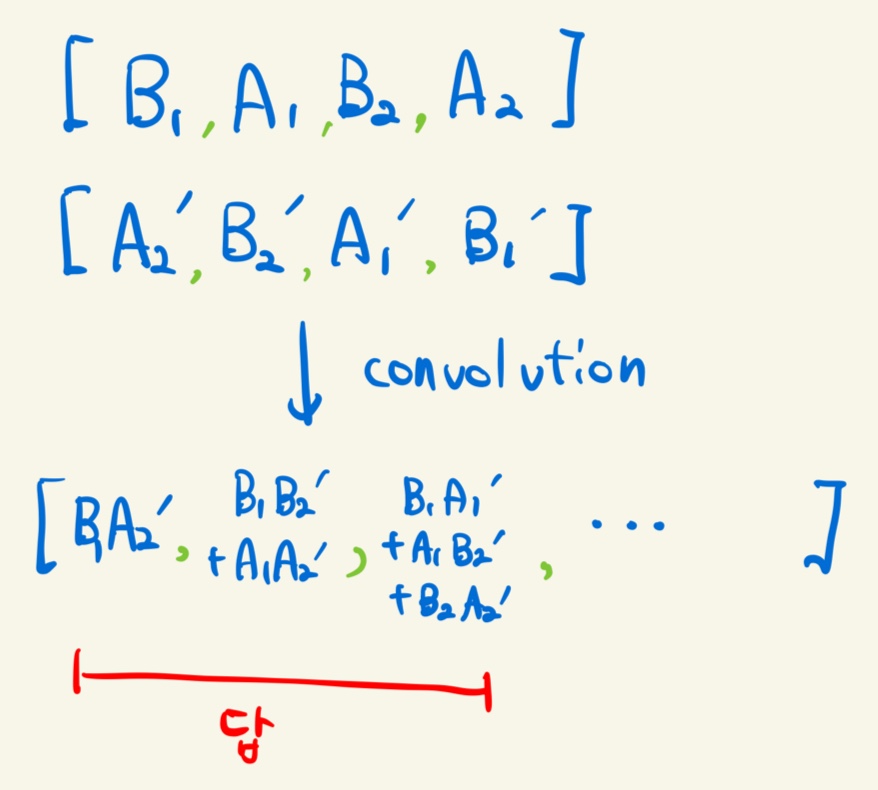
아래 스트링을 뒤집고 위 아래를 convolution한 결과를 보면 고맙게도 우리가 찾는 값들이 역순으로 저장되서 나온다는 사실을 알 수 있다. 이렇게 \(\scriptsize 0\) ~ \(\scriptsize N - 2\)번째 까지 계수를 역순으로 출력해주면 그게 정답이다. 이렇게 풀면, \(\scriptsize O(NlogN)\)에 문제 해결이 가능하다.
문제를 풀면서 느끼는건데.. FFT 문제들은 조금 뜬금없는 모델링을 필요로 한다는 느낌이다.