월반멘토링 2주차 set 풀이
30 Jul 2022보고 도움 되는 사람이 있는 것 같아서 계속 쓰려고요.. 오ㅋㅋ~
DFS / BFS / Backtracking
1. 소-난다! (Silver I)
tag : sieve of eratosthenes, primality test, dfs
아아.. 소난다.. 진짜 어지러운 문제 지문이다. 무슨 벌에 쏘이면 난다고 하질 않나..
하여튼, \(\scriptsize N\)개 중 \(\scriptsize M\)개를 골라 합을 만들고 그 값들 중 소수만 골라 출력해주면 되는 문제다.
조합을 다 만들어주면 되니까, \(\scriptsize O(\binom{N}{M})\) 에 해결 가능하다. 조합을 만드는 건 DFS로 할 수 있다. 어떤 원소를 뽑으면 카운트를 증가시키고 아니면 증가시키지 않도록 해서 M개가 될 때까지 값을 만들면 쉽게 합을 구할 수 있다.
모든 합을 구하고 나서는 그 값들이 소수인지만 봐주면 되는데, 이거는 대략 10,000까지 소수를(왜냐면, 최대 9000까지만 값이 나올 수 있거든요) 전처리 해두면 쉽게 해줄 수 있다. 전처리하는 방법은 에라토스테네스의 체를 사용해서 구하면 된다. 소수 판정을 가르친적이 없어서 이걸 넣으면 안됐을 것 같긴 한데.. 멘토 멘티님들 똑똑하시니까 잘 하셨을거라 믿는다.
풀이가 어렵진 않은데.. 실수할 수 있는 부분이 하나 있다면, 소수인 합이 하나도 안나올 수 있으니 그 경우에 예외처리를 잘 해주자.
코드 보기
#include <bits/stdc++.h>
using namespace std;
using ll = long long;
using pii = pair<int, int>;
using ppii = pair<int, pii>;
bool is_prime[10001];
set<int> cow_sum;
int cow[9];
int N, M;
void init_prime() {
fill(is_prime, is_prime + 10001, true);
is_prime[0] = is_prime[1] = false;
for(int i = 2; i <= sqrt(10000); ++i) {
if(is_prime[i]) {
for(int j = i * i; j <= 10000; j += i) {
is_prime[j] = false;
}
}
}
}
void dfs(int cur, int idx, int cnt) {
if(cnt == M) {
cow_sum.insert(cur);
return;
}
for(int i = idx; i < N; ++i) {
dfs(cur + cow[i], i + 1, cnt + 1);
dfs(cur, i + 1, cnt);
}
}
int main() {
ios_base::sync_with_stdio(false);
cin.tie(nullptr);
cout.tie(nullptr);
init_prime();
cin >> N >> M;
for(int i = 0; i < N; ++i) cin >> cow[i];
dfs(0, 0, 0);
int cnt = 0;
for(auto& c : cow_sum) {
if(is_prime[c]) {
cnt++;
cout << c << ' ';
}
}
if(cnt == 0) cout << "-1\n";
return 0;
}
2. 숨바꼭질 (Silver I)
tag : bfs
1번 노드부터 다른 모든 노드까지 거리를 구하면 풀 수 있다. 그래프 간선의 가중치가 모두 동일한 것으로 생각할 수 있으니까 거리는 BFS로 구할 수 있다. BFS로 1번노드로부터의 거리배열을 다 채워주자. 그런 이후 가장 먼 노드까지의 거리값을 가져온 뒤에 노드번호, 거리, 개수를 세어서 출력해주면 어렵지 않게 맞을 수 있다.
코드 보기
#include <bits/stdc++.h>
using namespace std;
using ll = long long;
using pii = pair<int, int>;
using ppii = pair<int, pii>;
vector<int> adj[20202];
int dist[20202];
const int INF = 1e9;
int ans_node, ans_dist, ans_cnt;
void solve() {
fill(dist, dist + 20202, -1);
queue<int> q;
dist[1] = 0;
q.push(1);
while(!q.empty()) {
int cur_node = q.front();
q.pop();
for(int& next_node : adj[cur_node]) {
if(dist[next_node] != -1) continue;
dist[next_node] = dist[cur_node] + 1;
q.push(next_node);
}
}
ans_dist = *max_element(dist, dist + 20202);
for(int i = 1; i <= 20202; ++i) {
if(dist[i] == ans_dist) {
ans_node = i;
break;
}
}
for(int i = 1; i <= 20202; ++i) {
if(dist[i] == ans_dist) ans_cnt++;
}
}
int main() {
ios_base::sync_with_stdio(false);
cin.tie(nullptr);
cout.tie(nullptr);
int N, M; cin >> N >> M;
for(int i = 0; i < M; ++i) {
int a, b; cin >> a >> b;
adj[a].push_back(b);
adj[b].push_back(a);
}
solve();
cout << ans_node << ' ' << ans_dist << ' ' << ans_cnt << '\n';
return 0;
}
3. 숨바꼭질 (Silver I)
tag : bfs
위 문제랑 이름만 같고 다른 문제다. 2번 문제는 다른분이 들고 오셨고 3번 문제는 내가 들고왔는데 모으고 나서 보니까 문제 이름이 같았던 우연..ㅎㅎ
문제 내용은 다른데 풀이는 비슷하다.
좌표를 전부 하나하나 노드로 봐주면 그래프 문제로 바뀐다. 헉! 그러면, 가중치가 같은 그래프 상에서 최단거리를 찾는 문제가 된다. 이는 마찬가지로 BFS로 해결할 수 있으니, 거리 배열을 만들고 다 채워넣어주자. BFS 종료 이후 K 인덱스 값에 접근해서 거리 값을 확인해 출력해주면 된다.
1년전 코드라 살짝 지저분한데 알아보는데는 무리 없을거라 생각해요. 히히
코드 보기
#include <iostream>
#include <queue>
#define INF 100000000
using namespace std;
bool isValid(int a) {
if(0 <= a && a <= 1000000) return true;
else return false;
}
int BFS(int N, int K) {
if(N == K) return 0;
int *cost;
cost = new int[1000001];
fill_n(cost, 1000001, INF);
queue<int> q;
q.push(N);
cost[N] = 0;
while(!q.empty()) {
int nowPoint = q.front();
q.pop();
int a = nowPoint - 1;
int b = nowPoint + 1;
int c = nowPoint * 2;
if(isValid(a) && cost[a] == INF) {
cost[a] = cost[nowPoint] + 1;
q.push(a);
}
if(isValid(b) && cost[b] == INF) {
cost[b] = cost[nowPoint] + 1;
q.push(b);
}
if(isValid(c) && cost[c] == INF) {
cost[c] = cost[nowPoint] + 1;
q.push(c);
}
if(a == K || b == K || c == K) {
int res = cost[K];
delete[] cost;
return res;
}
}
delete[] cost;
return -1;
}
int main() {
ios_base::sync_with_stdio(false);
cin.tie(nullptr);
int N, K;
cin >> N >> K;
cout << BFS(N, K);
return 0;
}
4. 스도쿠 (Gold IV)
tag : backtracking, implementation
스도쿠를 풀었다는 것은, 가로, 세로, 3 x 3영역에 1 ~ 9로 중복없이 다 채워졌다는 의미이다. 이걸 그대로 구현해주면 된다. 퍼즐이 0일때, 1 ~ 9부터 모조리 넣어보면서 중복이 없을 때, 다음칸으로 넘어가는 식으로 짜주면 된다.
말이 쉽지 백트래킹 처음 짜보면 엄청 어렵다는 거 알고 있으니.. 조금 더 자세히 설명해보겠습니다.
좌측 상단(0,0) 부터 칸을 채워나가기로 합시다. 항상 좌측에서 우측으로 이동하면서 값을 채우고 가장 오른쪽 끝에 도달하면 그 다음 행의 첫번째로 이동하도록 합시다.
- 숫자가 채워져 있으면 다음칸으로 넘어간다.
- 숫자가 채워져 있지 않으면 1 ~ 9의 값을 넣어보며 중복되지 않는 값을 넣어두고 다음칸으로 넘어간다.
- 이전에 잘못 채워져 있었으면 아무것도 값이 안들어가는 칸이 발생하는데.. 그럼 문제가 되었던 칸으로 다시 돌아가서 다른 값을 넣고 새로 시도한다. (이게 구현이 엄청 복잡해보이는데 재귀함수로 짜는거라 쉽게 해결할 수 있어요. 짜보면 이해할 수 있습니다.)
- 이 과정을 반복하면 스도쿠 해를 찾을 수 있다.
헉.. 이렇게 해서 해가 안찾아질 수 있는거 아닌가요? 생각할 수도 있는데 조금 머리를 많이 써서 생각해보면 모든 경우를 테스트하기 때문에 언제든 유효한 해가 나온다. 그냥 그렇다고 믿고 한 번 짜봅시다!
아래 코드도 한참 코드 못 짤때 짠거라 가독성이 별로 안좋은데.. 그래도 핵심 아이디어는 잘 알아들을 수 있을겁니다.
코드 보기
#include <iostream>
#include <vector>
using namespace std;
bool isEnd = false;
bool isOverlapped(int x, int y, vector<vector<int>>& map) {
bool check[10] = { false, };
for(int i = 0; i < 9; ++i) {
if(map[y][i]) {
if(check[map[y][i]]) return true;
check[map[y][i]] = true;
}
}
fill(check, check + 10, false);
for(int i = 0; i < 9; ++i) {
if(map[i][x]) {
if(check[map[i][x]]) return true;
check[map[i][x]] = true;
}
}
fill(check, check + 10, false);
int segX = x / 3;
int segY = y / 3;
for(int i = 0; i < 3; ++i) {
for(int j = 0; j < 3; ++j) {
if(map[3 * segY + i][3 * segX + j]) {
if(check[map[3 * segY + i][3 * segX + j]]) return true;
check[map[3 * segY + i][3 * segX + j]] = true;
}
}
}
return false;
}
void solve(int x, int y, vector<vector<int>>& map) {
if(isEnd) return;
if(x >= 9) {
x = 0;
y += 1;
}
if(x == 0 && y == 9) {
isEnd = true;
for(int i = 0; i < 9; ++i) {
for(int j = 0; j < 9; ++j) {
cout << map[i][j];
}
cout << '\n';
}
return;
}
if(map[y][x] == 0) {
for(int num = 1; num <= 9; ++num) {
map[y][x] = num;
if(!isOverlapped(x, y, map)) solve(x + 1, y, map);
map[y][x] = 0;
}
}
else solve(x + 1, y, map);
}
int main() {
ios_base::sync_with_stdio(false);
cin.tie(nullptr);
cout.tie(nullptr);
string str[9];
for(int i = 0; i < 9; ++i) cin >> str[i];
vector<vector<int>> map(9, vector<int>(9));
for(int i = 0; i < 9; ++i) {
for(int j = 0; j < 9; ++j) {
map[i][j] = str[i][j] - '0';
}
}
solve(0, 0, map);
return 0;
}
5. DSLR (Gold IV)
tag : implementation, bfs
DSLR 연산을 구현하고 A를 B로 변환하는 가장 빠른 명령어를 아무거나 하나 출력하는 문제다. 음.. 일단 이것도 마찬가지로 숫자 하나하나를 노드로 보면 그래프 문제로 바뀌고, 각 연산 또한 전부 가중치가 같은 간선으로 봐줄 수 있다. 즉, 가중치가 모두 동일한 그래프 상에서 최단거리를 찾고 최단거리를 만든 명령어를 역추적하는 문제다.
최단거리 찾는건 어찌저찌 할 수 있겠는데요.. 명령어는 어떻게 해야하죠? 가 사실 이 문제의 핵심이다. 나는 큐에 노드 번호뿐만 아니라, 명령어도 같이 삽입해서 B에 도달하면 해당 명령어를 출력하도록 했다.
한번, 탐색할 때마다 BFS로 10,000개의 노드만 보면 되니까 시간내에 잘 돌아갈거라 짐작할 수 있고 믿음을 가진채로 구현을 하면 AC를 받을 수 있다.
구현이 좀 난잡한데 여러분들은 이것보다 훨씬 간단하게 짤 수 있으니까 아이디어만 얻어가길 바랍니다 ㅎㅎ
코드 보기
// https://www.acmicpc.net/problem/9019 //
#include <iostream>
#include <string>
#include <utility>
#include <queue>
using namespace std;
string BFS(int A, int B) {
bool visit[10000];
fill_n(visit, 10000, false);
visit[A] = true;
queue<pair<int, string>> q;
q.push({ A, "" });
while(!q.empty()) {
pair<int, string> now = q.front();
int n = now.first;
string cmd = now.second;
q.pop();
//case D
if(2 * n <= 9999) {
if(!visit[2 * n]) {
if(2 * n == B) {
return (cmd + "D");
}
visit[2 * n] = true;
q.push({ 2 * n, cmd + "D" });
}
}
else {
if(!visit[(2 * n) % 10000]) {
if(((2 * n) % 10000) == B) {
return (cmd + "D");
}
visit[(2 * n) % 10000] = true;
q.push({ (2 * n) % 10000, cmd + "D" });
}
}
//case S
if(n != 0) {
if(!visit[n - 1]) {
if((n - 1) == B) {
return (cmd + "S");
}
visit[n - 1] = true;
q.push({ n - 1, cmd + "S" });
}
}
else {
if(!visit[9999]) {
if(9999 == B) {
return (cmd + "S");
}
visit[9999] = true;
q.push({ 9999, cmd + "S" });
}
}
int d1, d2, d3, d4;
d1 = (int)n / 1000;
d2 = (int)n / 100 - d1 * 10;
d3 = (int)n / 10 - d2 * 10 - d1 * 100;
d4 = n % 10;
int LShifted = ((d2 * 10 + d3) * 10 + d4) * 10 + d1;
int RShifted = ((d4 * 10 + d1) * 10 + d2) * 10 + d3;
//case L
if(!visit[LShifted]) {
if(LShifted == B) {
return (cmd + "L");
}
visit[LShifted] = true;
q.push({ LShifted, cmd + "L" });
}
//case R
if(!visit[RShifted]) {
if(RShifted == B) {
return (cmd + "R");
}
visit[RShifted] = true;
q.push({ RShifted, cmd + "R" });
}
}
}
int main() {
ios_base::sync_with_stdio(false);
cin.tie(nullptr);
cout.tie(nullptr);
int T;
cin >> T;
for(int i = 0; i < T; ++i) {
int A, B;
cin >> A >> B;
cout << BFS(A, B) << "\n";
}
return 0;
}
6. 벽 부수고 이동하기 (Gold IV)
tag : bfs
벽을 안부수고 이동한다면 그냥 평범한 BFS 문제다. 그런데… 벽을 하나 부술 수 있다고 한다. 그럼, BFS 돌다가 벽 만나면 해당 벽을 부순셈 치고 계속 BFS를 돌면 될까?
그렇게 쉽게는 안풀린다. 왜냐면 벽을 부수기 전과 벽을 부순 이후의 상태공간이 동일하지 않아서 그렇다. 벽을 부순 이후에는 아예 다른 공간이라서 방문체크도 새로 해줘야 한다. 벽을 부숨으로 경우의 수가 달라져 버린다고 생각하면 이해가 되려나? 예제를 몇개 직접 그려보면 내 얘기가 무슨 얘기인지 알 수 있을 것이다.
따라서, 벽을 부수기 전과 부순 이후의 상태공간이 달라서 방문 체크를 아예 새로 해줘야한다. 거리로 부순 이후로 새로 구해야 하고, 이런식으로 구한 값들을 모아서 최종적으로 한번 벽을 부수고 이동한 거리와 부수지 않고 이동한 거리를 서로 비교해 작은걸 출력해주면 된다. 부숴도 끝까지 못 이동하면 그건 -1을 출력해주면 된다.
자세한 이해는 코드를 보는게 편할 듯.. 이 문제에서는 벽을 한 번만 부수지만 이 원리를 확장시키면 벽 n개 부수는걸로도 확장할 수 있다.
코드 보기
// https://www.acmicpc.net/problem/2206 //
#include <iostream>
#include <vector>
#include <queue>
#include <tuple>
#include <string>
#define INF 987654321
using namespace std;
vector<vector<int>> map(1001, vector<int>(1001, -1));
vector<vector<int>> distA(1001, vector<int>(1001, INF));
vector<vector<int>> distB(1001, vector<int>(1001, INF));
vector<vector<bool>> visitA(1001, vector<bool>(1001, false));
vector<vector<bool>> visitB(1001, vector<bool>(1001, false));
void solve(int& N, int& M) {
int dx[4] = {1, 0, -1, 0};
int dy[4] = {0, 1, 0, -1};
queue<tuple<int, int, int>> q;
distA[1][1] = 1;
visitA[1][1] = true;
q.push({1, 1, 0});
while(!q.empty()) {
int x = get<0>(q.front());
int y = get<1>(q.front());
int breaked = get<2>(q.front());
q.pop();
for(int i = 0; i < 4; ++i) {
int nx = x + dx[i];
int ny = y + dy[i];
if(nx <= 0 || nx > M || ny <= 0 || ny > N) continue; //coord check
if(breaked == 1 && map[ny][nx] == 1) continue; //map check
if(breaked == 0 && !visitA[ny][nx]) {
if(map[ny][nx] == 1) {
visitB[y][x] = true;
visitB[ny][nx] = true;
distB[ny][nx] = distA[y][x] + 1;
q.push({nx, ny, 1});
}
else {
distA[ny][nx] = distA[y][x] + 1;
visitA[ny][nx] = true;
q.push({nx, ny , 0});
}
}
else if(breaked == 1 && !visitB[ny][nx]) {
visitB[ny][nx] = true;
distB[ny][nx] = distB[y][x] + 1;
q.push({nx, ny, 1});
}
}
}
if((distA[N][M] == INF) && (distB[N][M] == INF)) cout << "-1";
else cout << min(distA[N][M], distB[N][M]);
}
int main() {
int N, M; cin >> N >> M;
for(int i = 1; i <= N; ++i) {
string tmp; cin >> tmp;
for(int j = 1; j <= M; ++j) {
map[i][j] = (tmp[j - 1] - '0');
}
}
solve(N, M);
return 0;
}
7. 육각형 우리 속의 개미 (Gold III)
tag : dfs, backtracking
육각형으로 움직여야하는 이상한 형태를 띄는 문제다. 문제 해결 방법이 다양할 것 같은데, 나는 방향벡터 6개를 만들어 움직이는 식으로 문제를 해결했다. 아래 그림을 참고하자.
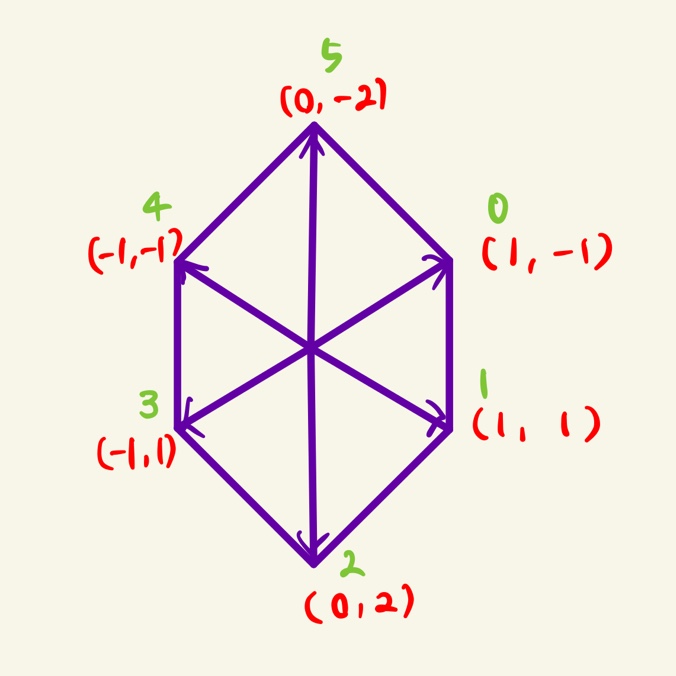
어떤 \(\scriptsize i\)번 방향으로 움직이면 그 다음 방향은 \(\scriptsize (i - 1) \mod 6\)와 \(\scriptsize (i + 1) \mod 6\)이다. 이런 성질 덕분에 다음 움직일 방향을 쉽게 찾을 수 있다.
\(dfs(y, x, dir) :=\) “(y, x)부터 dir방향으로 갔을 때, N만큼 회전한 길이를 경로를 찾는 함수”
라고 정의하면, dfs함수를 사용해서 개수를 구할 수 있다. 한번 회전할 때 2가지 경우 밖에 없으므로 \(\scriptsize 2^{N}\)의 경우의 수만 확인하면 되고 \(\scriptsize N\)이 작기 때문에 시간 내에 답을 구할 수 있다.
자세한 구현은 코드를 참고!
코드 보기
#include <bits/stdc++.h>
using namespace std;
using ll = long long;
using pii = pair<int, int>;
using ppii = pair<int, pii>;
int dx[6] = {1, 1, 0, -1, -1, 0};
int dy[6] = {-1, 1, 2, 1, -1, -2};
bool vst[101][101];
int ans;
int N;
pii next_dir(int dir) {
int next_1 = (dir + 1) % 6;
int next_2 = (dir + 5) % 6;
return {next_1, next_2};
}
void DFS(int y, int x, int dir, int cnt) {
int ny = y + dy[dir];
int nx = x + dx[dir];
if(vst[ny][nx]) {
if(cnt == N) ans++;
return;
}
if(cnt >= N) return;
vst[ny][nx] = true;
pii d = next_dir(dir);
DFS(ny, nx, d.first, cnt + 1);
DFS(ny, nx, d.second, cnt + 1);
vst[ny][nx] = false;
}
int main() {
ios_base::sync_with_stdio(false);
cin.tie(nullptr);
cout.tie(nullptr);
cin >> N;
vst[48][50] = true;
DFS(48, 50, 5, 0);
cout << ans << '\n';
return 0;
}
8. 트리의 지름 (Gold II)
tag : dfs, ad-hoc..?
어느 트리 정점으로부터 가장 멀리 떨어진 리프노드로 이동하자. 그 리프노드로부터 가장 멀리 떨어진 리프노드를 찾아보자. 그럼 그 거리가 지름이 된다.
예?
누가봐도 가장 긴 거리가 맞다.
증명은 다른 분들이 잘 해주셨으니 찾아서 공부하시면 됩니다! 구현은 DFS 2번이면 쉽게 구할 수 있습니다.
- 임의의 노드로부터 가장 멀리 떨어진 노드로 이동
- 해당 노드로부터 가장 멀리 떨어진 노드까지의 길이 리턴
만 하면 끝!
코드 보기
// https://www.acmicpc.net/problem/1167 //
#include <iostream>
#include <queue>
#include <vector>
using namespace std;
vector<pair<int, int>> adj[100001];
void treeDist(int n) {
vector<bool> visit(100001, false);
vector<int> dist(100001, 0);
queue<int> q;
visit[1] = true;
q.push(1);
while(!q.empty()) {
int now = q.front();
q.pop();
for(auto element : adj[now]) {
if(visit[element.first]) continue;
dist[element.first] = dist[now] + element.second;
visit[element.first] = true;
q.push(element.first);
}
}
int maxIdx = 1;
int maximum = 0;
for(int i = 1; i <= n; ++i) {
if(dist[i] > maximum) {
maximum = dist[i];
maxIdx = i;
}
}
fill(visit.begin(), visit.end(), false);
fill(dist.begin(), dist.end(), 0);
visit[maxIdx] = true;
q.push(maxIdx);
while(!q.empty()) {
int now = q.front();
q.pop();
for(auto element : adj[now]) {
if(visit[element.first]) continue;
dist[element.first] = dist[now] + element.second;
visit[element.first] = true;
q.push(element.first);
}
}
maximum = 0;
for(int i = 1; i <= n; ++i) {
if(dist[i] > maximum) {
maximum = dist[i];
}
}
cout << maximum;
}
int main() {
int n; cin >> n;
for(int i = 1; i <= n; ++i) {
int st; cin >> st;
while(true) {
int ed; cin >> ed;
if(ed == -1) break;
int w; cin >> w;
adj[st].push_back({ed, w});
adj[ed].push_back({st, w});
}
}
treeDist(n);
return 0;
}
9. 수식 트리 (Gold I)
tag : dfs
숫자말고 변수로 한 번 생각해보자. 예제로 설명을 해보자면, 수식 트리를 잘 따라가서 식을 정리하면, a - b + c - d + e 처럼 뭔가 부호가 붙어 있는 식으로 나온다. 양수는 양수끼리 음수는 음수끼리 정리한다고 치면, (a + c + e) - (d + e) 처럼 정리 가능 하다. 그럼 그리디하게 앞에는 큰 수들을 넣고 뒤엔 작은 수를 넣으면 항상 값이 최대가 된다. 헉! 이제 문제가 바꼈다. 중요한 건 마이너스 부호가 붙은 노드의 개수이니 그 개수만을 알아오면 된다.
트리를 잘 쳐다보자. 마이너스 연산자의 오른쪽 자식은 변수의 부호가 바뀐다. 왼쪽 자식은 그대로다. 플러스 연산자는 부호가 안바뀐다. 이건 DFS로 잘 구현하면 된다. 부호가 바뀔 때만 주의해서, 리프 노드에 도달하면 해당 부호를 반영해주고 DFS를 완료하면 음수 개수를 카운팅하자.
오름차순으로 정렬해서 카운팅한 갯수만큼은 \(\scriptsize neg\)에 더하고, 나머지는 \(\scriptsize pos\)에 더한 뒤 \(\scriptsize pos - neg\)를 출력하면 된다.
코드 보기
#include <bits/stdc++.h>
using namespace std;
using ll = long long;
using pii = pair<int, int>;
using ppii = pair<int, pii>;
struct node {
bool is_minus;
int left, right;
} tree[202020];
bool neg_count[101010];
int N;
void DFS(int node, bool is_neg) {
if(1 <= node && node <= N) {
neg_count[node] = is_neg;
return;
}
DFS(tree[node].right, (tree[node].is_minus ? !is_neg : is_neg));
DFS(tree[node].left, is_neg);
}
int main() {
ios_base::sync_with_stdio(false);
cin.tie(nullptr);
cout.tie(nullptr);
cin >> N;
vector<ll> seq(N);
for(ll& e : seq) cin >> e;
for(int i = N + 1; i <= 2 * N - 1; ++i) {
char c; cin >> c;
int l, r; cin >> l >> r;
if(c == '-') tree[i].is_minus = true;
tree[i].left = l, tree[i].right = r;
}
DFS(2 * N - 1, false);
int cnt = 0;
for(int i = 1; i <= N; ++i) if(neg_count[i]) cnt++;
ll neg = 0;
sort(seq.begin(), seq.end());
for(int i = 0; i < cnt; ++i)
neg += seq[i];
ll pos = 0;
for(int i = cnt; i < N; ++i)
pos += seq[i];
cout << pos - neg << '\n';
return 0;
}